题目内容
1.(1)求不等式x2-4x+3≤0的解集;(2)求函数y=x+$\frac{4}{x}$的值域.
分析 (1)原不等式等价于(x-1)(x-3)≤0,即可得出不等式x2-4x+3≤0的解集;
(2)分类讨论,利用基本不等式,即可求函数y=x+$\frac{4}{x}$的值域.
解答 解:(1)原不等式等价于(x-1)(x-3)≤0,
所以不等式的解为1≤x≤3,
即不等式x2-4x+3≤0的解集为{x|1≤x≤3}.…(5分)
(2)当x>0时,y=x+$\frac{4}{x}$≥4,当且仅当x=$\frac{4}{x}$,即x=2时等号成立;
当x<0时,y=-(-x+$\frac{4}{-x}$)≤4,当且仅当-x=$\frac{4}{-x}$,即x=-2时等号成立
∴函数y=x+$\frac{4}{x}$的值域为{y|y≥4,或y≤-4}.…(10分)
点评 本题考查不等式的解法,考查基本不等式的运用,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
17.已知数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,设数列{an}的前n项和为Sn,则S2017=( )
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
13.若集合A={x|2x>x2},B={y|y=2x,x∈A},则集合A∩B等于( )
| A. | (0,2) | B. | (0,4) | C. | (1,2) | D. | (0,+∞) |
11.某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为X元,求X的分布列和数学期望E(X).
| 消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
| 收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
| 消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 频数 | 60 | 20 | 10 | 5 | 5 |
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为X元,求X的分布列和数学期望E(X).
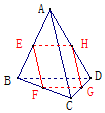 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,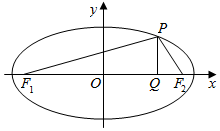 已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.
已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.