题目内容
5.已知函数f(x)=2exln$\sqrt{e}$-kx(e=2.17128…是自然对数的底数)有两个不同的零点,则实数k的取值范围是( )| A. | (0,+∞) | B. | [1,+∞) | C. | (e,+∞) | D. | (1,+∞) |
分析 求导f′(x)=a-ex,由导数判断函数的单调性,根据图象与横轴交点个数即可判定零点个数.
解答 解:函数f(x)=2exln$\sqrt{e}$-kx=f(x)=ex-kx 其定义域为:R
f′(x)=k-ex.
当k≤0时,f′(x)<0,f(x)在R上单调递减,最多存在一个零点,不满足条件;
当k>0时,由f′(x)=0解得x=lnk,
当x>lnk时,f′(x)<0,当x<lnk时,f′(x)>0.
故f(x)在x=lnk处取得最大值f(lnk)=alnk-k,
∵f(x)存在两个零点,
∴f(lnk)=alnk-k>0,
k>e,即a的取值范围是(e,+∞).
故选:C.
点评 本题考查了导数的综合应用及零点问题,属于中档题

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
13.若a>b,则下列正确的是( )
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
20.下列对应是集合A到集合B的映射的是( )
| A. | A=N*,B=N*,f:x→|x-3| | |
| B. | A={平面内的圆},B={平面内的三角形},f:作圆的内接三角形 | |
| C. | A={x|0≤x≤2},B={y|0≤y≤6},f:x→y=$\frac{1}{2}x$ | |
| D. | A={0,1},B={-1,0,1},f:A中的数开平方根 |
10.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )
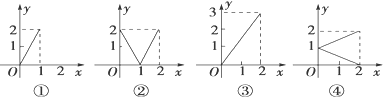

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.已知数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,设数列{an}的前n项和为Sn,则S2017=( )
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
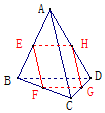 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,