题目内容
8.设关于x的一元二次方程x2+2ax+b2=0,若a是从区间[0,4]上任取的一个数,b是从区间[0,3]上任取的一个数,求上述方程有实根的概率.分析 本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤4,0≤b≤3},而构成事件A的区域为{(a,b)|0≤a≤4,0≤b≤3,a≥b},根据几何概型公式得到结果.
解答 解:设事件A为“方程x2+2ax+b2=0有实根”.
则△=4a2-4b2≥0,即a2≥b2.
又∵a≥0,b≥0,
∴a≥b.
试验的全部结果所构成的区域为{(a,b)|0≤a≤4,0≤b≤3},而构成事件A的区域为{(a,b)|0≤a≤4,0≤b≤3,a≥b},即如图所示的阴影部分: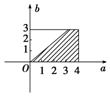
∴P(A)=$\frac{3×4-\frac{1}{2}×{3}^{2}}{4×3}$=$\frac{5}{8}$.
点评 本题给出含有字母参数的一元二次方程,求方程有实数根的概率.着重考查了一元二次方程根的判别式、不等式表示的平面区域、面积公式和几何概型计算公式等知识,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
13.若a>b,则下列正确的是( )
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
20.下列对应是集合A到集合B的映射的是( )
| A. | A=N*,B=N*,f:x→|x-3| | |
| B. | A={平面内的圆},B={平面内的三角形},f:作圆的内接三角形 | |
| C. | A={x|0≤x≤2},B={y|0≤y≤6},f:x→y=$\frac{1}{2}x$ | |
| D. | A={0,1},B={-1,0,1},f:A中的数开平方根 |
17.已知数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,设数列{an}的前n项和为Sn,则S2017=( )
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
13.若集合A={x|2x>x2},B={y|y=2x,x∈A},则集合A∩B等于( )
| A. | (0,2) | B. | (0,4) | C. | (1,2) | D. | (0,+∞) |
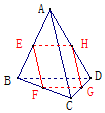 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,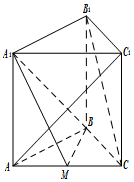 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$