题目内容
1.已知轴截面为正方形 EFGH 的圆柱的体积为2π,则从点E沿圆柱的侧面到相对顶点 G的最短距离是$\sqrt{{π}^{2}+4}$.分析 由题意轴截面为正方形 EFGH 的圆柱的体积为2π,正方形的边长为1.可以从E点沿圆柱的侧面到相对顶点G的最短距离为圆柱侧面展开图一个顶点到对边中点的距离,利用勾股定理就可以求出其值.
解答 解:轴截面为正方形 EFGH 的圆柱的体积为2π,正方形的边长为1
从E点沿圆柱的侧面到相对顶点G的最短距离即为圆柱侧面展开图一个顶点到对边中点的距离,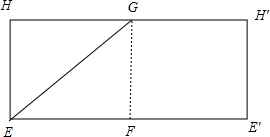
∵圆柱的轴截面的边长为1,
故GF=2,EF=π,
∴EG=$\sqrt{{π}^{2}+4}$,
故答案为:$\sqrt{{π}^{2}+4}$.
点评 本题考查的知识点是旋转体的展开图,其中将问题转化为平面上两点之间的距离线段最短是解答的关键.

练习册系列答案
相关题目
11.复数Z=$\frac{-2i}{1+2i}$(i为虚数单位)所对应复平面内的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.从学号为1至50的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |
13.若a>b,则下列正确的是( )
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
10.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )
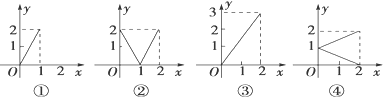

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
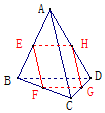 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,