Question

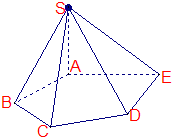如图，在五棱锥S-ABCDE中，SA⊥底面ABCDE，SA=AB=AE=2，BC=DE=

3

，∠BAE=∠BCD=∠CDE=120°
（1）证明：CD∥平面SBE；
（2）证明：平面SBC⊥平面SAB．

Answer 1

考点：平面与平面垂直的判定,直线与平面平行的判定

专题：证明题,空间位置关系与距离

分析：（1）连结BE，延长BC、ED交于点F，证明BE∥CD，即可证明CD∥平面SBE；
（2）利用线面垂直的判定，证明BC⊥平面SAB，即可证明平面SBC⊥平面SAB．

解答： 证明：（1）连结BE，延长BC、ED交于点F，则∠DCF=∠CDF=60°，
∴△CDF为正三角形，∴CF=DF
又BC=DE，∴BF=EF，
因此，△BFE为正三角形，
∴∠FBE=∠FCD=60°，∴BE∥CD，
∵CD?平面SBE，BE?平面SBE，
∴CD∥平面SBE．
（2）由题意，△ABE为等腰三角形，∠BAE=120°，
∴∠ABE=30°，又∠FBE=60°，
∴∠ABC=90°，∴BC⊥BA
∵SA⊥底面ABCDE，BC?底面ABCDE，
∴SA⊥BC，
又SA∩BA=A，
∴BC⊥平面SAB  
又BC?平面SBC
∴平面SBC⊥平面SAB．

点评：本题考查直线与平面平行，平面与平面垂直的判定，考查学生空间想象能力，逻辑思维能力，是中档题．