题目内容
在正方形ABCD中,E、F分别在AB、BC边上,且BE=BF=
BC,将△AED和△CFD分别沿DE、DF折起,使A、C两点重合于点P,连接EF、PB.
(1)求证:PD⊥EF;
(2)求异面直线PB和EF所成角的大小;
(3)求证:点P在平面EFD上的射影不可能落在EF上.
| 1 |
| 4 |
(1)求证:PD⊥EF;
(2)求异面直线PB和EF所成角的大小;
(3)求证:点P在平面EFD上的射影不可能落在EF上.
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由PD⊥PE,PD⊥PF,得PD⊥平面PEF,由此能证明PD⊥EF.
(2)由BE=BF=BC,EF∥AC,AC⊥BD,EF⊥BD,EF⊥PD,由此能求出异面直线PB和EF所成的角为90°.
(3)假设点P在平面EFD上的射影G落在EF上,PG⊥EF,PE=PF,点G必为EF的中点,BD与EF的交点为G.由此能推导出与平面内过一点有且只有一条直线与已知直线垂直矛盾,从而得到点P在平面EFD上的射影不可能落在EF上.
(2)由BE=BF=BC,EF∥AC,AC⊥BD,EF⊥BD,EF⊥PD,由此能求出异面直线PB和EF所成的角为90°.
(3)假设点P在平面EFD上的射影G落在EF上,PG⊥EF,PE=PF,点G必为EF的中点,BD与EF的交点为G.由此能推导出与平面内过一点有且只有一条直线与已知直线垂直矛盾,从而得到点P在平面EFD上的射影不可能落在EF上.
解答:
(1)证明:PD⊥PE,PD⊥PF,PE∩PF=P,
∴PD⊥平面PEF.又EF?平面PEF,
∴PD⊥EF.
(2)解:BE=BF=BC,EF∥AC,
又AC⊥BD,EF⊥BD,
又EF⊥PD,BD∩PD=D,
EF⊥平面PBD.又PB?平面PBD,∴EF⊥PB,
∴异面直线PB和EF所成的角为90°.
(3)证明:假设点P在平面EFD上的射影G落在EF上,
PG⊥EF,PE=PF,点G必为EF的中点,
即BD与EF的交点为G.
由点在面内的射影的定义知PG⊥面EFD,PG⊥GD,
又DP⊥面PEF,PG⊥面PEF,DP⊥PG.
又GD∩DP=D,这与平面内过一点有且只有一条直线与已知直线垂直矛盾,
上述假设不成立,即点P在平面EFD上的射影不可能落在EF上.
∴PD⊥平面PEF.又EF?平面PEF,
∴PD⊥EF.
(2)解:BE=BF=BC,EF∥AC,
又AC⊥BD,EF⊥BD,
又EF⊥PD,BD∩PD=D,
EF⊥平面PBD.又PB?平面PBD,∴EF⊥PB,
∴异面直线PB和EF所成的角为90°.
(3)证明:假设点P在平面EFD上的射影G落在EF上,
PG⊥EF,PE=PF,点G必为EF的中点,
即BD与EF的交点为G.
由点在面内的射影的定义知PG⊥面EFD,PG⊥GD,
又DP⊥面PEF,PG⊥面PEF,DP⊥PG.
又GD∩DP=D,这与平面内过一点有且只有一条直线与已知直线垂直矛盾,
上述假设不成立,即点P在平面EFD上的射影不可能落在EF上.
点评:本题考查异面直线垂直的证明,考查异面直线所成角的大小的求法,考查点P在平面上的射影不可能落在直线上的证明,解题时要注意空间思维能力的培养.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
函数y=log
(x+
+5)(x>1)的最大值为( )
| 1 |
| 2 |
| 1 |
| x-1 |
| A、4 | B、3 | C、-4 | D、-3 |
圆C:x2+y2-4=0被直线l:x-y+2=0截得的弦长为( )
A、2
| ||
B、
| ||
C、
| ||
D、2
|
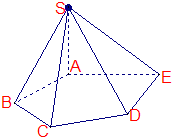 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=