题目内容
对向量
=(a1,a2),
=(b1,b2)定义一种运算“⊕”:a?b=(a1,a2)⊕(b1,b2)=(a1b1,a2b2),已知动点P,Q分别在曲线y=sinx和y=f(x)上运动,且
=m⊕
+m(其中O为坐标原点),若向量
=(
,3),
=(
,0),则y=f(x)的最大值为 .
| a |
| b |
| OQ |
| Op |
| m |
| 1 |
| 2 |
| n |
| π |
| 6 |
考点:进行简单的合情推理,平面向量数量积的运算
专题:新定义,平面向量及应用,推理和证明
分析:可设P(s,t),Q(x,y),则t=sins,由条件可得,(x,y)=(
s,3t)+(
,0),x=
s+
,且y=3t,即有s=2(x-
),且t=
,即y=f(x)=3sin(2x-
).由正弦函数的最大值,即可得到答案.
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| y |
| 3 |
| π |
| 3 |
解答:
解:由于动点P,Q分别在曲线y=sinx和y=f(x)上运动,
可设P(s,t),Q(x,y),则t=sins,
由于
=
⊕
+
(其中O为坐标原点),向量
=(
,3),
=(
,0),
则由新定义可得,(x,y)=(
s,3t)+(
,0)
则有x=
s+
,且y=3t,即有s=2(x-
),且t=
,
即y=f(x)=3sin(2x-
).
由于x∈R,则f(x)的最大值为3.
故答案为:3.
可设P(s,t),Q(x,y),则t=sins,
由于
| OQ |
| m |
| Op |
| n |
| m |
| 1 |
| 2 |
| n |
| π |
| 6 |
则由新定义可得,(x,y)=(
| 1 |
| 2 |
| π |
| 6 |
则有x=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| y |
| 3 |
即y=f(x)=3sin(2x-
| π |
| 3 |
由于x∈R,则f(x)的最大值为3.
故答案为:3.
点评:本题考查新定义的理解和运用,考查三角函数的最值,以及平面向量的运算,属于中档题.

练习册系列答案
相关题目
已知一函数满足x>0时,有g′(x)=2x2>
,则下列结论一定成立的是( )
| g(x) |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
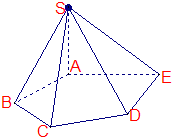 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=