题目内容
O点为圆O的圆心,点A,B在圆O上,且点A在第一象限,点B(-
,
),点C为圆O与x轴正半轴的交点,设∠COB=θ,求sin2θ的值.
| 3 |
| 5 |
| 4 |
| 5 |
考点:二倍角的正弦,任意角的三角函数的定义
专题:高考数学专题,三角函数的求值,三角函数的图像与性质
分析:由点B的坐标可知θ为第二象限角,利用同角三角函数间基本关系求出sinθ,cosθ的值,sin2θ利用二倍角的正弦函数公式化简后,将各自的值代入计算即可求出值.
解答:
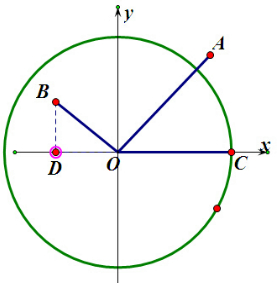 解:如图,∵点B(-
解:如图,∵点B(-
,
),点C为圆O与x轴正半轴的交点,设∠COB=θ,
∴cos(π-θ)=
=-cosθ,sin(π-θ)=
∴cosθ=-
,sinθ=
,
∴sin2θ=2sinθcosθ=2×
×(-
)=-
 解:如图,∵点B(-
解:如图,∵点B(-| 3 |
| 5 |
| 4 |
| 5 |
∴cos(π-θ)=
| 4 |
| 5 |
| 3 |
| 5 |
∴cosθ=-
| 4 |
| 5 |
| 3 |
| 5 |
∴sin2θ=2sinθcosθ=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
点评:本题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
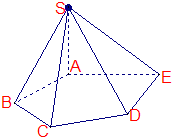 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=