题目内容
已知a、b、c是△ABC的三内角A、B、C的对边，且a=1，b=4，
•
=1．
（Ⅰ）求c；
（Ⅱ）求sin（C+
）．
| CA |
| CB |
（Ⅰ）求c；
（Ⅱ）求sin（C+
| π |
| 3 |
考点：平面向量数量积的运算,两角和与差的正弦函数
专题：平面向量及应用
分析：（Ⅰ）根据数量积的计算公式可求得cosC=
，根据余弦定理即可求出c；
（Ⅱ）先求出sinC，根据两角和的正弦公式即可求出sin（C+
）．
| 1 |
| 4 |
（Ⅱ）先求出sinC，根据两角和的正弦公式即可求出sin（C+
| π |
| 3 |
解答：
解：（Ⅰ）
•
=4cosC=1，∴cosC=
；
由余弦定理得：c2=a2+b2-2abcosC=1+16-2=15；
∴c=
；
（Ⅱ）sinC=
=
；
∴sin(C+
)=sinCcos
+cosCsin
=
+
=
．
| CA |
| CB |
| 1 |
| 4 |
由余弦定理得：c2=a2+b2-2abcosC=1+16-2=15；
∴c=
| 15 |
（Ⅱ）sinC=
1-
|
| ||
| 4 |
∴sin(C+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 8 |
| ||
| 8 |
| ||||
| 8 |
点评：考查数量积的计算公式，余弦定理，两角和的正弦公式．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
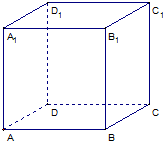如图，在正方体ABCD-A1B1C1D1中，E，F分别为AB、AD的中点，
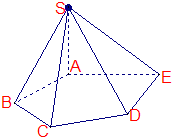如图，在五棱锥S-ABCDE中，SA⊥底面ABCDE，SA=AB=AE=2，BC=DE=