题目内容
若奇函数f(x)在区间[2,5]上的最小值是5,那么f(-x)在区间[-5,-2]上有( )
| A、最小值-5 | B、最小值5 |
| C、最大值-5 | D、最大值5 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用奇函数的性质:奇函数图象关于原点对称可得正确选项.
解答:
解:∵奇函数图象关于原点对称,并且奇函数f(x)在区间[2,5]上的最小值是5,
∴f(x) 在区间[-5,-2]上有最大值-5;
∴f(-x)=-f(x)在区间[-5,-2]上有最小值5.
故选:B.
∴f(x) 在区间[-5,-2]上有最大值-5;
∴f(-x)=-f(x)在区间[-5,-2]上有最小值5.
故选:B.
点评:本题考查了奇函数的图象性质;奇函数图象关于原点成中心对称,并且对称区间的单调性相同.

练习册系列答案
相关题目
函数y=log
(x+
+5)(x>1)的最大值为( )
| 1 |
| 2 |
| 1 |
| x-1 |
| A、4 | B、3 | C、-4 | D、-3 |
已知一函数满足x>0时,有g′(x)=2x2>
,则下列结论一定成立的是( )
| g(x) |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
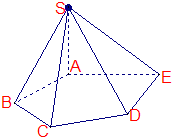 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE= 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: