题目内容
8.数列{an}对于确定的正整数m,若存在正整数n使得am+n=am+an成立,则称数列{an}为“m阶可分拆数列”.(1)设{an}是首项为2,公差为2的等差数列,证明{an}为“3阶可分拆数列”;
(2)设数列{an}的前n项和为${S_n}={2^n}-a$(a>0),若数列{an}为“1阶可分拆数列”,求实数a的值;
(3)设${a_n}={2^n}+{n^2}+12$,试探求是否存在m使得若数列{an}为“m阶可分拆数列”.若存在,请求出所有m,若不存在,请说明理由.
分析 (1)an=2n.可得a3+n=a3+an.即可证明{an}为“3阶可分拆数列”.
(2)${S_n}={2^n}-a$(a>0),a1=S1=2-a,n≥2时,an=Sn-Sn-1=2n-1.根据数列{an}为“1阶可分拆数列”,可得an+1=a1+an,可得a.
(3)假设数列{an}为“m阶可分拆数列”.可得am+n=am+an成立,化为(2m-1)(2n-1)+2mn=13.对m,n分类讨论即可得出.
解答 (1)证明:an=2+2(n-1)=2n.
则a3+n=2×(3+n)=6+2n=a3+an.
∴{an}为“3阶可分拆数列”.
(2)解:${S_n}={2^n}-a$(a>0),a1=S1=2-a,n≥2时,an=Sn-Sn-1=2n-a-(2n-1-a)=2n-1.
∵数列{an}为“1阶可分拆数列”,
∴an+1=a1+an,∴2n=2-a+2n-1,∴a=2-2n-1.
令n=1时,a=1.
(3)解:假设数列{an}为“m阶可分拆数列”.
则am+n=am+an成立,∴2n+m+(n+m)2+12=2m+m2+12+2n+n2+12,
化为:2n+m+2mn=2m+2n+12,
∴(2m-1)(2n-1)+2mn=13.
可得:m=1,n=3;m=2,n不存在;m=3,n=1.m≥4时n不存在.
∴只有两组:m=1,n=3;m=3,n=1.
点评 本题考查了数列递推关系、新定义、分类讨论方法、数列通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知x,y满足$\left\{\begin{array}{l}{x+y-2≥0}\\{x+2y-4≥0}\\{x-3≤0}\end{array}\right.$,则3x+4y的最小值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 11 |
13.已知向量$\vec a$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$与向量$\overrightarrow{a}$+2$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
17.函数y=2sin2(x+$\frac{3π}{2}$)-1是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
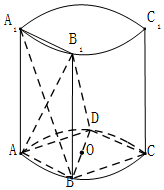 如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.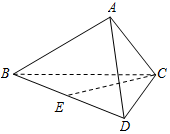 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.