题目内容
16.已知α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π),sinα=$\frac{3}{5}$,sin(α+β)=-$\frac{4}{5}$,则sinβ=$-\frac{7}{25}$.分析 构造思想,sinβ=sin[(α+β)-α],再利用和与差公式直接求解即可.
解答 解:α∈(0,$\frac{π}{2}$),sinα=$\frac{3}{5}$
可得:cosα=$\frac{4}{5}$
∵β∈($\frac{π}{2}$,π),
∴α+β∈($\frac{π}{2},\frac{3π}{2}$),
又sin(α+β)=-$\frac{4}{5}$<0,
∴cos(α+β)=-$\frac{3}{5}$
则sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$-\frac{7}{25}$.
故答案为$-\frac{7}{25}$
点评 本题考查了构造思想,和与差公式的运用和计算能力.属于基础题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
13.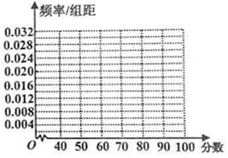 学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:
学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:
(Ⅰ)请在答题卡上完成频率分布表和作出频率分布直方图;
(Ⅱ)用样本估计总体,若高三年级共有2000人,估计成绩不及格(60分以下)的人数;
(Ⅲ)为了帮助成绩差的学生提高数学成绩,现从成绩[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学,即成立帮扶学习小组,样本中已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
 学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:
学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:| 分组 | 频数 | 频率 |
| [40,50) | 2 | |
| [50,60) | 3 | |
| [60,70) | 0.28 | |
| [70,80) | 15 | |
| [80,90) | 12 | |
| [90,100] | 4 |
(Ⅱ)用样本估计总体,若高三年级共有2000人,估计成绩不及格(60分以下)的人数;
(Ⅲ)为了帮助成绩差的学生提高数学成绩,现从成绩[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学,即成立帮扶学习小组,样本中已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
11.已知数列{an}为等比数列,且a2013+a2015=$\int_0^2{\sqrt{4-{x^2}}}$dx,则a2014(a2012+2a2014+a2016)的值为( )
| A. | π2 | B. | 4π2 | C. | π | D. | 2π |
5.设i为虚数单位,若$z=\frac{a-i}{1+i}(a∈{R})$是纯虚数,则a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
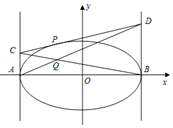 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.