题目内容
18.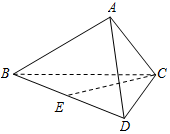 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.(1)求证:AB⊥AD;
(2)设E是BD的中点,若直线CE与平面ACD的夹角为30°,求四面体ABCD外接球的表面积.
分析 (1)证明DC⊥BC,AB⊥CD,推出AB⊥AC,然后证明AB⊥平面ADC,得到AB⊥AD.
(2)取AD的中点F,连接EF,则EF∥BA,证明EF⊥平面ADC,连接FC,说明∠ECF=30°,求出以四面体ABCD的外接球的半径然后求解即可.
解答 解:(1)证明:由平面ABC⊥平面BCD,DC⊥BC,得DC⊥平面ABC,∴AB⊥CD…(2分)
又由$AB=\sqrt{3}$,BC=2,AC=1,得BC2=AB2+AC2,所以AB⊥AC…(4分)
故AB⊥平面ADC,所以AB⊥AD…(6分)
(2)取AD的中点F,连接EF,则EF∥BA,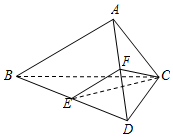
因为AB⊥平面ADC∴EF⊥平面ADC…(8分)
连接FC,则∠ECF=30°,∴$CE=2EF=AB=\sqrt{3}$…(9分)
又∠BAD=∠BCD=90°,
所以四面体ABCD的外接球的半径$R=CE=\sqrt{3}$…(11分)
故四面体ABCD的外接球的表面积=$4π{(\sqrt{3})^2}=12π$…(12分)
(向量解法酌情给分)
点评 本题考查直线与平面垂直的判定定理的应用,几何体的外接球的表面积的求法,直线与平面所成角的应用,考查空间想象能力以及计算能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
10.设复数z满足$\frac{{{{({1+i})}^2}}}{z}=1-i$,则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
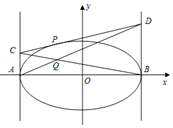 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.