题目内容
20.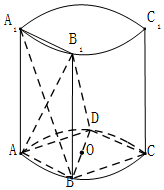 如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.(Ⅰ)证明:BC⊥AB1;
(Ⅱ)(ⅰ)求二面角A1-BB1-D的大小;
(ⅱ)求异面直线AB1和BD所成角的余弦值.
分析 (Ⅰ)证明:BC⊥平面A1B1BA,即可证明BC⊥AB1;
(Ⅱ)(ⅰ)以C为原点,以$\overrightarrow{CD}$、$\overrightarrow{CB}$、$\overrightarrow{C{C_1}}$为x轴、y轴、z轴正方向建立空间直角坐标系C-xyz,不妨设圆柱的高为2,求出平的法向量,即可求二面角A1-BB1-D的大小;
(ⅱ)求出向量的坐标,即可求异面直线AB1和BD所成角的余弦值.
解答 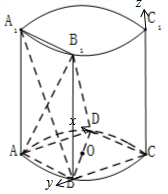 (Ⅰ)证明:因为B1B⊥平面ABCD,且BC?平面ABCD,所以BC⊥B1B,
(Ⅰ)证明:因为B1B⊥平面ABCD,且BC?平面ABCD,所以BC⊥B1B,
又因为在底面圆O中,AB⊥BC,AB∩B1B=B,所以BC⊥平面A1B1BA,
又因为BA1?平面A1B1BA,所以BC⊥AB1.…(5分)
(Ⅱ)解:(ⅰ)由圆柱性质知CB、CD、CC1两两垂直.
以C为原点,以$\overrightarrow{CD}$、$\overrightarrow{CB}$、$\overrightarrow{C{C_1}}$为x轴、y轴、z轴正方向建立空间直角坐标系C-xyz,不妨设圆柱的高为2.
则C(0,0,0),$B(0,\sqrt{2},0)$,O(1,1,0).…6分
所以平面A1B1B的一个法向量是$\overrightarrow{CB}=(0,\sqrt{2},0)$.
平面BB1D的一个法向量是$\overrightarrow{CO}=(1,1,0)$.
所以$cos<\overrightarrow{CB},\overrightarrow{CO}>=\frac{{\overrightarrow{CB}•\overrightarrow{CO}}}{{|{\overrightarrow{CB}}||{\overrightarrow{CO}}|}}=\frac{{\sqrt{2}}}{{\sqrt{2}×\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$.…(8分)
由图知二面角A1-BB1-D是锐二面角,所以它的大小是$\frac{π}{4}$.…(9分)
(ⅱ)由题意得$A(\sqrt{2},\sqrt{2},0)$,$D(\sqrt{2},0,0)$,${B_1}(0,\sqrt{2},2)$.
所以$\overrightarrow{A{B_1}}=(-\sqrt{2},0,2)$,$\overrightarrow{BD}=(\sqrt{2},-\sqrt{2},0)$.
所以$|{cos<\overrightarrow{A{B_1}},\overrightarrow{BD}>}|=\frac{{|{\overrightarrow{A{B_1}}•\overrightarrow{BD}}|}}{{|{\overrightarrow{A{B_1}}}||{\overrightarrow{BD}}|}}=\frac{{|{-2}|}}{{\sqrt{2+4}\sqrt{2+2}}}=\frac{{\sqrt{6}}}{6}$. …(12分)
点评 本题考查线面垂直的判定与性质,考查面面角,考查异面直线所成角,考查向量知识的运用,属于中档题.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | π2 | B. | 4π2 | C. | π | D. | 2π |
| A. | (1,2) | B. | [$\frac{1}{2},1$] | C. | ($\frac{1}{2},1$) | D. | (2,3) |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |