Question

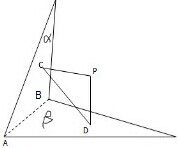已知P是二面角α-AB-β内一点，PC⊥α，垂足为C，PD⊥β，垂足为D，且PC=3，PD=4，∠CPD=60°，求：
（1）二面角α-AB-β的大小；
（2）CD的长．

Answer 1

考点：二面角的平面角及求法

专题：空间位置关系与距离,空间角

分析：设平面PCD交AB于E，连CE，DE．由已知得PC⊥CE，PC⊥AB，PD⊥DE．PD⊥AB，从而∠CED是二面角α-AB-β的平面角，由此能求出二面角α-AB-β的大小．
2．在△PCD中，由PC=3，PD=4，∠CPD=60°，能求出CD．

解答： 解：（1）设平面PCD交AB于E，连CE，DE．
∵PC⊥α，
∴PC⊥CE，PC⊥AB，
同理，PD⊥DE．PD⊥AB，
∴AB⊥平面PCD，
∴∠CED是二面角α-AB-β的平面角．
又∠CPD=60°，
∴二面角α-AB-β的大小为120°．
（2）在△PCD中，PC=3，PD=4，∠CPD=60°，
CD²=9+16-12=13，
∴CD=

13

．

点评：本题考查二面角的大小的求法，考查线段长的求法，解题时要认真审题，注意空间思维能力的培养．