题目内容
已知数列{an}的通项公式是an=n2sin(
π),则a1+a2+a3+…+a2014=( )
| 2n+1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出a1+a2+a3+…+a2014=(22-12)+(42-32)+(62-52)+…+(20142-20132),由此能求出结果.
解答:
解:∵an=n2sin(
π)=
,
∴a1+a2+a3+…+a2014
=(22-12)+(42-32)+(62-52)+…+(20142-20132)
=1+2+3+4+5+6+…+2013+2014
=
.
故选:B.
| 2n+1 |
| 2 |
|
∴a1+a2+a3+…+a2014
=(22-12)+(42-32)+(62-52)+…+(20142-20132)
=1+2+3+4+5+6+…+2013+2014
=
| 2014×2015 |
| 2 |
故选:B.
点评:本题考查数列的前2014项和的求法,是中档题,解题时要认真审题,注意an=n2sin(
π)=
的合理运用.
| 2n+1 |
| 2 |
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
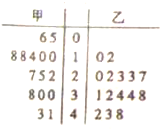 从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为
从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法中不正确的是( )
A、对于线性回归方程
| ||||||||||
| B、茎叶图的优点在于它可以保存原始数据,并且可以随时记录 | ||||||||||
| C、将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变 | ||||||||||
D、掷一枚均匀硬币出现正面向上的概率是
|
已知双曲线
-
=1(a>0,b>0)的右焦点与抛物线y2=12x的焦点重合,且双曲线的一条渐近线被圆(x-3)2+y2=8截得的弦长为4,则此双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±2
|
一批产品分为一、二、三级,其中一级品是二级品的2倍,三级品为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量ξ,则Eξ的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
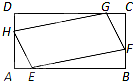 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
 已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为3
已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为3