题目内容
已知函数f（x）=-x3+3x2+9x+a，求f（x）的单调递减区间．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，解f′（x）＜0，即可得到结论．
解答：
解：∵f（x）=-x3+3x2+9x+a，
∴f′（x）=-3x2+6x+9，
由f′（x）=-3x2+6x+9＜0，
即x2-2x-3＞0，解得x＞3或x＜-1，
即函数的单调递减区间为（3，+∞），（-∞，-1）．
∴f′（x）=-3x2+6x+9，
由f′（x）=-3x2+6x+9＜0，
即x2-2x-3＞0，解得x＞3或x＜-1，
即函数的单调递减区间为（3，+∞），（-∞，-1）．
点评：本题主要考查函数单调区间的求解，求函数的导数，利用导数和单调性之间的关系是解决本题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
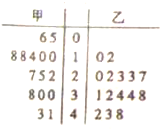从甲乙两个城市分别随机抽取15台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的右焦点与抛物线y2=12x的焦点重合，且双曲线的一条渐近线被圆（x-3）2+y2=8截得的弦长为4，则此双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±2
|
设∠A，∠B，∠C是△ABC的三个内角，且tanA、
、tanB成等差数列，tanA、
、tanB成等比数列，则△ABC是（ ）
| 5 |
| 12 |
| ||
| 6 |
| A、锐角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |