题目内容
 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是①AC∥平面DA1C1;
②BD1⊥平面DA1C1;
③过点B与异面直线AC和A1D所成角均为60°;
④四面体DA1D1C1与ABCD-A1B1C1D1的内切球半径之比为
| ||
| 3 |
⑤与平面DA1C1平行的平面与正方体的各个面都有交点,则这个截面的周长为定值.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:①由于AC∥A1C1,利用线面平行的判定定理即可判断出AC∥平面DA1C1;
②由于BD1⊥A1D,BD1⊥C1D,利用线面垂直的判定定理可得BD1⊥平面DA1C1;
③由于异面直线AC和A1D所成的角为60°,可得过点B与异面直线AC和A1D所成的角均为60°的直线有且只有1条.
④设AA1=a,可求得四面体DA1D1C1内切球半径为
a,而正方体ABCD-A1B1C1D1的内切球半径为
a,即可得出所求的比.
⑤将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
a(a为正方体的棱长).
②由于BD1⊥A1D,BD1⊥C1D,利用线面垂直的判定定理可得BD1⊥平面DA1C1;
③由于异面直线AC和A1D所成的角为60°,可得过点B与异面直线AC和A1D所成的角均为60°的直线有且只有1条.
④设AA1=a,可求得四面体DA1D1C1内切球半径为
| 1 | ||
3+
|
| 1 |
| 2 |
⑤将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
| 2 |
解答:
 解:①∵AC∥A1C1,AC?平面A1C1D,A1C1?平面A1C1D,∴AC∥平面DA1C1,因此①正确;
解:①∵AC∥A1C1,AC?平面A1C1D,A1C1?平面A1C1D,∴AC∥平面DA1C1,因此①正确;
②BD1⊥A1D,BD1⊥C1D,A1D∩C1D=D,∴BD1⊥平面DA1C1,因此②正确;
③∵异面直线AC和A1D所成的角为60°,∴过点B与异面直线AC和A1D所成的角均为60°的直线有且只有1条.故③错误.
④设AA1=a,可求得四面体DA1D1C1内切球半径为
a,而正方体ABCD-A1B1C1D1的内切球半径为
a,故所求的比应为1-
.故④错误.
⑤将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
a(a为正方体的棱长),故⑤正确.
综上可知:正确的有①、②、⑤.
故答案为:①②⑤.
 解:①∵AC∥A1C1,AC?平面A1C1D,A1C1?平面A1C1D,∴AC∥平面DA1C1,因此①正确;
解:①∵AC∥A1C1,AC?平面A1C1D,A1C1?平面A1C1D,∴AC∥平面DA1C1,因此①正确;②BD1⊥A1D,BD1⊥C1D,A1D∩C1D=D,∴BD1⊥平面DA1C1,因此②正确;
③∵异面直线AC和A1D所成的角为60°,∴过点B与异面直线AC和A1D所成的角均为60°的直线有且只有1条.故③错误.
④设AA1=a,可求得四面体DA1D1C1内切球半径为
| 1 | ||
3+
|
| 1 |
| 2 |
| ||
| 3 |
⑤将正方体沿D1A1、A1B1、B1C、CD、DD1展开到一个平面上,如图所示,易知截面多边形EFGHIJ的周长为定值,等于3
| 2 |
综上可知:正确的有①、②、⑤.
故答案为:①②⑤.
点评:本题综合考查了线面平行于垂直的判定定理和性质定理、异面直线所成的角、内切球的性质、展开图等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的右焦点与抛物线y2=12x的焦点重合,且双曲线的一条渐近线被圆(x-3)2+y2=8截得的弦长为4,则此双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±2
|
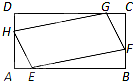 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为