题目内容
已知O为锐角△ABC的外心,AB=6,AC=10,
=x
+y
,且2x+10y=5,则边BC的长为 .
| AO |
| AB |
| AC |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由于三角形外心与三角形边的中点的连线,与这条边垂直,所以分别取边AB,AC的中点D,E,并连接OD,OE.由于AO是△AOD和△AOE的公共边,现在Rt△AOD中,cos∠OAD=
=
•
,这样表示出cos∠OAD之后,再求一下
•
,结果求出来是18,同样的办法去求
•
.对
=x
+y
的两边同乘以
,会得到关于x,y,cos∠BAC的一个等式;同样的办法,对其两边同乘以
,又可以得到一个等式,结合条件2x+10y=5便可解出cos∠BAC.这时候,就可以用余弦定理求BC边了.
|
| ||
|
|
| 1 |
| 2 |
|
| ||
|
|
| AO |
| AB |
| AO |
| AC |
| AO |
| AB |
| AC |
| AB |
| AC |
解答:
解:分别取AB,AC的中点为D,E,并连接OD,OE,根据条件有:OD⊥AB,OE⊥AC;
在Rt△OAD中,cos∠OAD=
=
•
=
;
∴
•
=|
||
|cos∠OAD=|
|•6•
=18;
同理可得,
•
=50;
∴
•
=x
•
+y
•
=36x+60ycos∠BAC ①
•
=x
•
+y
•
=60xcos∠BAC+100y ②
又2x+10y=5 ③
∴由①②③解得cos∠BAC=
;
由余弦定理得:BC2=36+100-2×6×10×
=96,∴BC=4
.
故答案为:4
.
在Rt△OAD中,cos∠OAD=
|
| ||
|
|
| 1 |
| 2 |
|
| ||
|
|
| 3 | ||
|
|

∴
| AO |
| AB |
| AO |
| AB |
| AO |
| 3 | ||
|
|
同理可得,
| AO |
| AC |
∴
| AO |
| AB |
| AB |
| AB |
| AC |
| AB |
| AO |
| AC |
| AB |
| AC |
| AC |
| AC |
又2x+10y=5 ③
∴由①②③解得cos∠BAC=
| 1 |
| 3 |
由余弦定理得:BC2=36+100-2×6×10×
| 1 |
| 3 |
| 6 |
故答案为:4
| 6 |
点评:求解本题的关键就是求
•
,
•
,并对
=x
+y
的两边分别乘以
,
,所以这样就会出现cos∠BAC,然后建立关于cos∠BAC的等式,从而解出它来.
| AO |
| AB |
| AO |
| AC |
| AO |
| AB |
| AC |
| AB |
| AC |

练习册系列答案
相关题目
一批产品分为一、二、三级,其中一级品是二级品的2倍,三级品为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量ξ,则Eξ的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
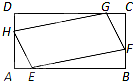 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为