题目内容
4.已知向量$\overrightarrow a=(\sqrt{3}sinωx,cosωx),\overrightarrow b=(cosωx,-cosωx),(ω>0)$,函数f(x)=$\overrightarrow a•\overrightarrow b+\frac{1}{2}$的图象的两相邻对称轴间的距离为$\frac{π}{4}$.(1)求ω的值;
(2)若$x∈(\frac{7π}{24},\frac{5π}{12})$,f(x)=-$\frac{3}{5}$,求cos4x的值;
(3)是否存在实数a使得af(x)+1≥0在$x∈[0,\frac{π}{4}]$上恒成立?若存在请求出a的取值,若不存在请说明理由.
分析 (1)先根据向量的数量积和二倍角公式和两角的差的正弦公式,以及周期的定义即可求出,
(2)根据同角的三角函数的关系和两角和余弦公式即可求出,
(3)先求出f(x)的范围,再分类讨论即可求出a的取值范围
解答 解:(1)由题意,$f(x)=\sqrt{3}sinωx•cosωx-{cos^2}ωx+\frac{1}{2}$=$\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1+cos2ωx}{2}+\frac{1}{2}$=$\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1}{2}cos2ωx$=$sin(2ωx-\frac{π}{6})$,
∵两相邻对称轴间的距离为$\frac{π}{4}$,
∴$T=\frac{2π}{2ω}=\frac{π}{2}$,
∴ω=2.
(2)由(1)得,$f(x)=sin(4x-\frac{π}{6})=-\frac{3}{5}$,
∵$x∈(\frac{7π}{24},\frac{5π}{12})$,∴$4x-\frac{π}{6}∈(π,\frac{3}{2}π)$,
∴$cos(4x-\frac{π}{6})=-\frac{4}{5}$,
∴$cos4x=cos(4x-\frac{π}{6}+\frac{π}{6})$=$cos(4x-\frac{π}{6})cos\frac{π}{6}-sin(4x-\frac{π}{6})sin\frac{π}{6}$=$(-\frac{4}{5})×\frac{{\sqrt{3}}}{2}-(-\frac{3}{5})×\frac{1}{2}$=$-\frac{{2\sqrt{3}}}{5}+\frac{3}{10}$.
(3)由f(x)=sin(4x-$\frac{π}{6}$)
∵$x∈[0,\frac{π}{4}]$,
∴4x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5}{6}$π],
∴f(x)∈[-$\frac{1}{2}$,1],
∵实数a使得af(x)+1≥0在$x∈[0,\frac{π}{4}]$上恒成立,
当f(x)∈[-$\frac{1}{2}$,0)时,a≤-$\frac{1}{f(x)}$,即a≤2,
当f(x)∈(0,1],a≥$\frac{1}{f(x)}$,即a≥1,
当f(x)=0时,a取任何数都成立,
综上所述a的取值范围为[1,2]
点评 本题考查向量的数量数量积的运算和三角函数的化简以及正弦函数的图象和性质和函数的恒成立的问题,属于中档题

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
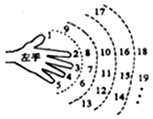 某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.
某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.