题目内容
13.已知函数f(x)=sin2(3x-$\frac{π}{6}$),求函数y=f(x)在x=$\frac{π}{6}$处的切线方程.分析 求出函数的导数,分别求出f($\frac{π}{6}$),f′($\frac{π}{6}$)的值,求出切线方程即可.
解答 解:f(x)=sin2(3x-$\frac{π}{6}$)=$\frac{1-cos(6x-\frac{π}{3})}{2}$,f($\frac{π}{6}$)=$\frac{3}{4}$,
f′(x)=3sin(6x-$\frac{π}{3}$),则f′($\frac{π}{6}$)=$\frac{3\sqrt{3}}{2}$,
故在x=$\frac{π}{6}$处的切线方程为y-$\frac{3}{4}$=$\frac{3\sqrt{3}}{2}$(x-$\frac{π}{6}$),
整理得:$\frac{3\sqrt{3}}{2}$x-y-$\frac{\sqrt{3}}{4}$π+$\frac{3}{4}$=0.
点评 本题考查了切线方程问题,考查导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.对具有线性相关关系的变量x,y,测得一组数据如下:
根据以上数据,利用最小二乘法得它们的回归直线方程为$\stackrel{∧}{y}$=10.5x+$\stackrel{∧}{a}$,据此模型来预测当x=20时,y的估计值为211.5.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
3.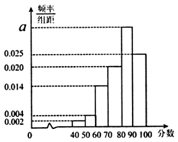 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
已知满意度等级为基本满意的有136人.
(I)求表中a的值及不满意的人数;
(II)特从等级为不满意师生中按评分分层抽取6人了解不满意的原因,并从6人中选取2人担任整改监督员,求2人中恰有1人评分在[40,50)的概率;
(III)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”,根据你所学的统计知识,判断是否能获奖,并说明理由.(注:满意指数=$\frac{满意程度的平均分}{100}$)
 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
(I)求表中a的值及不满意的人数;
(II)特从等级为不满意师生中按评分分层抽取6人了解不满意的原因,并从6人中选取2人担任整改监督员,求2人中恰有1人评分在[40,50)的概率;
(III)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”,根据你所学的统计知识,判断是否能获奖,并说明理由.(注:满意指数=$\frac{满意程度的平均分}{100}$)



