题目内容
14.已知f(x)=-$\frac{{3{x^2}}}{2}$+lnx,g(x)=$\frac{1}{2}{x^2}$-2ax+1+lnx.(Ⅰ)求函数f(x)的极值.
(Ⅱ)若x0是函数g(x)的极大值点,证明:x0lnx0-ax02>-1.
分析 (Ⅰ)求出导数,讨论导数的符号,确定其单调区间,从而确定极值.
(Ⅱ)g(x)定义域是(0,+∞),$g'(x)=x+\frac{1}{x}-2a$.分以下两种情况讨论,①若a≤1,②若a>1.
解答 解:(Ⅰ)f(x)定义域是(0,+∞),$f'(x)=\frac{{1-3{x^2}}}{x}$,令f'(x)=0得$x=\frac{{\sqrt{3}}}{3}$.
列表
| x | $(0,\frac{{\sqrt{3}}}{3})$ | $\frac{{\sqrt{3}}}{3}$ | (0,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | $-\frac{1}{2}-\frac{1}{2}ln3$ | ↘ |
(Ⅱ)g(x)定义域是(0,+∞),$g'(x)=x+\frac{1}{x}-2a$.…(6分)
①若a≤1,$g'(x)=x+\frac{1}{x}-2a≥2-2a≥0$,g(x)单调递增无极值点,不符合题意…(8分)
②若a>1,g'(x)=0即x2-2ax+1=0有两个不等的实数根x1和x2(x1<x2),因为x1x2=1,x1+x2=2a>0,所以0<x1<1<x2.
当0<x<x1时,g'(x)>0,当x1<x<x2时,g'(x)<0,当x>x2时,g'(x)>0,
所以g(x)在(0,x1)单调递增,在(x1,x2)单调递减,在(x2,+∞)单调递增.所以x0=x1为函数f(x)的极大值点,且0<x1<1.
因为g'(x1)=0,所以$a=\frac{{{x_1}^2+1}}{{2{x_1}}}$.
所以${x_1}ln{x_1}-a{x_1}^2$=${x_1}ln{x_1}-\frac{{{x_1}^3+{x_1}}}{2}$=$-\frac{{{x_1}^3}}{2}-\frac{1}{2}{x_1}+{x_1}ln{x_1}$,x1∈(0,1).
令$h(x)=-\frac{x^3}{2}-\frac{1}{2}x+xlnx$,x∈(0,1),$h'(x)=f(x)+\frac{1}{2}$.
由(Ⅰ)可知$f(x)+\frac{1}{2}≤f(\frac{{\sqrt{3}}}{3})+\frac{1}{2}=-\frac{1}{2}ln\sqrt{3}<0$,所以h(x)在(0,1)上单调递减,
故h(x)>h(1)=-1,原题得证.…(12分)
点评 本题考查了导数的综合应用,利用导数求极值、最值,考查了计算能力,属于压轴题,

练习册系列答案
相关题目
19.已知$f(x)=\sqrt{3}sinxcosx-{sin^2}x$,把f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移$\frac{1}{2}$个单位,得到y=g(x)的图象,则( )
| A. | g(x)为奇函数 | B. | g(x)为偶函数 | ||
| C. | g(x)在$[0,\frac{π}{3}]$上单调递增 | D. | g(x)的一个对称中心为$(-\frac{π}{2},0)$ |
6.已知边长为$2\sqrt{2}$的正方形ABCD的四个顶点都在球心为O的球面上,若球O的体积为36π,则直线OA与平面ABCD所成的角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
3.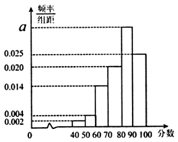 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
已知满意度等级为基本满意的有136人.
(I)求表中a的值及不满意的人数;
(II)特从等级为不满意师生中按评分分层抽取6人了解不满意的原因,并从6人中选取2人担任整改监督员,求2人中恰有1人评分在[40,50)的概率;
(III)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”,根据你所学的统计知识,判断是否能获奖,并说明理由.(注:满意指数=$\frac{满意程度的平均分}{100}$)
 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
(I)求表中a的值及不满意的人数;
(II)特从等级为不满意师生中按评分分层抽取6人了解不满意的原因,并从6人中选取2人担任整改监督员,求2人中恰有1人评分在[40,50)的概率;
(III)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”,根据你所学的统计知识,判断是否能获奖,并说明理由.(注:满意指数=$\frac{满意程度的平均分}{100}$)



