Question

已知集合A={（x，y）|x-y+b=0}与集合B={（x，y）|

4x-x2

+y-3=0}，若A∩B是单元素集合，则b的取值范围是（　　）

• A、{1-2

  2

  ，1+2

  2

  }
• B、（1-2

  2

  ，3]
• C、（-1，3]
• D、（-1，3]∪{1-2

  2

  }

Answer 1

考点：交集及其运算

专题：集合

分析：集合A表示直线x-y+b=0的图象，集合B表示（x-2）²+（y-3）²=4的下半圆，抓住三个关键点，直线过A，B，直线与半圆相切，求出A与B交集是单元素集合时b的范围即可．

解答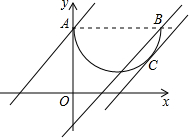： 解：集合A表示直线x-y+b=0的图象，集合B表示（x-2）²+（y-3）²=4的下半圆，
当直线x-y+b=0过A（0，3）时，将A坐标代入直线方程得：b=3；
当直线x-y+b=0过B（4，3）时，将B坐标代入直线方程得：b=-1；
当直线x-y+b=0与半圆相切于点C时，圆心（2，3）到直线的距离d=r=2，即

|2-3+b|

2

=2，
解得：b=1-2

2

或b=1+2

2

（舍去），
综上，若A∩B是单元素集合，b的取值范围是（-1，3]∪{1-2

2

}．
故选：D．

点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．