题目内容
15.设f'(x)是函数y=f(x)的导数,f''(x)是f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设f(x)=$\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}$x+1,数列{an}的通项公式为an=2n-7,则f(a1)+f(a2)+…+f(a8)=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由题意对已知函数求两次导数可得图象关于点(2,1)对称,即f(x)+f(4-x)=2,即可得到结论.
解答 解:∵f(x)=$\frac{1}{3}{x^3}-2{x^2}+\frac{8}{3}$x+1,
∴f′(x)=x2-4x+$\frac{8}{3}$,
∴f′(x)=2x-4,
令f″(x)=0,解得:x=2,
而f(2)=$\frac{8}{3}$-8+$\frac{8}{3}$×2+1=1,
故函数f(x)关于点(2,1)对称,
∴f(x)+f(4-x)=2,
∵an=2n-7,
∴a1=-5,a8=9,
∴f(a1)+f(a8)=2,
同理可得f(a2)+f(a7)=2,f(a3)+f(a6)=2,f(a4)+f(a5)=2,
∴f(a1)+f(a2)+…+f(a8)=2×4=8,
故选:D
点评 本题主要考查导数的基本运算,利用条件求出函数的对称中心是解决本题的关键.求和的过程中使用了倒序相加法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知公比q≠1的等比数列{an}前n项和Sn,a1=1,S3=3a3,则S5=( )
| A. | 1 | B. | 5 | C. | $\frac{31}{48}$ | D. | $\frac{11}{16}$ |
10.已知x,y是[0,1]上的两个随机数,则x,y满足y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2作直线A,B交双曲线右支于A,B两点,若|AF1|+|BF1|的最小值为11a,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
4.已知集合A={x|y=lg(x+1)},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | {-2,-1} | B. | {-2} | C. | {-1,0,1} | D. | {0,1} |
5.已知向量$\overrightarrow{OA}=({3,1}),\overrightarrow{OB}=({-1,3})$,$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}({m>0,n>0})$,若m+n=1,则$|{\overrightarrow{OC}}$|的最小值为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
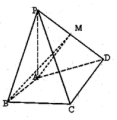 在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.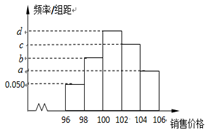 某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.
某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.