题目内容
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2作直线A,B交双曲线右支于A,B两点,若|AF1|+|BF1|的最小值为11a,则双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由题意可得,当直线AB与x轴垂直时,|AF1|+|BF1|的最小,根据F2的坐标,求出|AB|=$\frac{2{b}^{2}}{a}$,再根据双曲线的定义可得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{7}{2}$,再根据离心率公式计算即可.
解答 解:由题意可得,当直线AB与x轴垂直时,|AF1|+|BF1|的最小,
又F2=(c,0),
∴$\frac{{c}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
解得y=±$\frac{{b}^{2}}{a}$,
∴|AB|=$\frac{2{b}^{2}}{a}$,
∵|AF1|+|BF1|-|AB|=4a,
∴11a-$\frac{2{b}^{2}}{a}$=4a,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{7}{2}$,
∴e=$\frac{{c}^{2}}{{a}^{2}}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{7}{2}}$=$\frac{3\sqrt{2}}{2}$,
故选:C.
点评 本题考查了双曲线的性质和定义,考查了学生的转化能力和运算能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如图是一个算法的程序框图,如果输入i=0,S=0,那么输出的结果为( )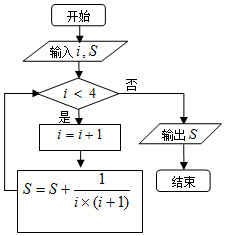

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
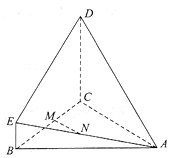 如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.
如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.