题目内容
已知直线l1的参数方程为:
,t为参数.
(1)将直线l1的参数方程化成直线的普通方程(写成一般式);
(2)已知直线l2:x+y-2=0,判断l1与l2是否相交,如果相交,请求出交点坐标.
|
(1)将直线l1的参数方程化成直线的普通方程(写成一般式);
(2)已知直线l2:x+y-2=0,判断l1与l2是否相交,如果相交,请求出交点坐标.
考点:直线的参数方程
专题:坐标系和参数方程
分析:(1)将参数方程
消去参数t,化为普通方程.
(2)两直线斜率不相同,因此它们相交,再把这两条直线的方程联立方程
,求得它们的交点的坐标.
|
(2)两直线斜率不相同,因此它们相交,再把这两条直线的方程联立方程
|
解答:
解:(1)将参数方程
化为普通方程:x+2y-7=0.
(2)两直线斜率不相同,因此它们相交,下面求它们的求点坐标:
联立方程
,解得:
,
可得交点的坐标为(-3,5).
|
(2)两直线斜率不相同,因此它们相交,下面求它们的求点坐标:
联立方程
|
|
可得交点的坐标为(-3,5).
点评:本题主要考查把参数方程化为普通方程的方法,求两条曲线的交点坐标,属于基础题.

练习册系列答案
相关题目
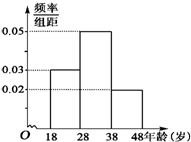 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.