题目内容
已知函数f(x)=
(x>0).
(Ⅰ)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(Ⅱ)若f(x)>
?x∈(0,+∞)恒成立,求正整数k的最大值.
| 1+ln(x+1) |
| x |
(Ⅰ)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(Ⅱ)若f(x)>
| k |
| x+1 |
考点:函数恒成立问题,函数的单调性及单调区间
专题:综合题,导数的综合应用
分析:(Ⅰ)利用导数的符号即可作出判断;
(Ⅱ)f(x)>
恒成立,化为h(x)=
>k恒成立,即h(x)的最小值大于k.求导h′(x)=
,记g(x)=x-1-ln(x+1)(x>0),利用导数可判断g(x)的单调性及g(x)的零点所在区间,进而可得h(x)的最小值,得到k的范围,由此可求最小正整数k.
(Ⅱ)f(x)>
| k |
| x+1 |
| (x+1)[1+ln(x+1)] |
| x |
| x-1-ln(x+1) |
| x2 |
解答:
解:(Ⅰ)f(x)在(0,+∞)上是减函数.证明如下:
f′(x)=
[
-1-ln(x+1)]=-
[
+ln(x+1)],
∵x>0,∴x2>0,
>0,ln(x+1)>0,∴f′(x)<0,
∴f(x)在(0,+∞)上是减函数.
(Ⅱ)f(x)>
恒成立,即h(x)=
>k恒成立,即h(x)的最小值大于k.
h′(x)=
,记g(x)=x-1-ln(x+1)(x>0),
则g′(x)=
>0,∴g(x)在(0,+∞)上单调递增,
又g(2)=1-ln3<0,g(3)=2-2ln2>0,
∴g(x)=0存在唯一实根a,且满足a∈(2,3),g(a)=0,即a=1+ln(a+1),
当x>a时,g(x)>0,h′(x)>0,当0<x<a时,g(x)<0,h′(x)<0,
∴h(x)min=h(a)=
=a+1∈(3,4),
∴k<a+1,
故正整数k的最大值为3.
f′(x)=
| 1 |
| x2 |
| x |
| x+1 |
| 1 |
| x2 |
| 1 |
| x+1 |
∵x>0,∴x2>0,
| 1 |
| x+1 |
∴f(x)在(0,+∞)上是减函数.
(Ⅱ)f(x)>
| k |
| x+1 |
| (x+1)[1+ln(x+1)] |
| x |
h′(x)=
| x-1-ln(x+1) |
| x2 |
则g′(x)=
| x |
| x+1 |
又g(2)=1-ln3<0,g(3)=2-2ln2>0,
∴g(x)=0存在唯一实根a,且满足a∈(2,3),g(a)=0,即a=1+ln(a+1),
当x>a时,g(x)>0,h′(x)>0,当0<x<a时,g(x)<0,h′(x)<0,
∴h(x)min=h(a)=
| (a+1)[1+ln(a+1)] |
| a |
∴k<a+1,
故正整数k的最大值为3.
点评:该题考查利用导数研究函数的单调性、最值及函数恒成立问题,考查转化思想,考查学生灵活运用知识分析解决问题的能力.

练习册系列答案
相关题目
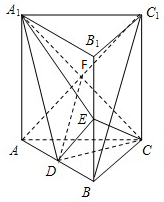 如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,
如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,