题目内容
 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.(1)求直方图中x的值;
(2)求续驶里程在[200,300]的车辆数;
(3)若从续驶里程在[200,300]的车辆中随机抽取2辆车,记ξ表示续驶里程在[250,300)的车辆数,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由频率分布直方图,能求出x=0.003.
(2)由(2)及题意能求出续驶里程在[200,300]的车辆数5.
(3)由(2)及题意知,续驶里程在[200,250]的车辆数为3,续驶里程在[250,300]的车辆数为2,ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(2)由(2)及题意能求出续驶里程在[200,300]的车辆数5.
(3)由(2)及题意知,续驶里程在[200,250]的车辆数为3,续驶里程在[250,300]的车辆数为2,ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答:
解:(1)由频率分布直方图,得:
(0.002+0.005+0.008+x+0.002)×50=1,
解得x=0.003.
(2)由(2)及题意知续驶里程在[200,300]的车辆数为:
20×(0.003×50+0.002×50)=5.
(3)由(2)及题意知,续驶里程在[200,250]的车辆数为3,
续驶里程在[250,300]的车辆数为2,
ξ的可能取值为0,1,2,
∴P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴ξ的分布列为:
Eξ=0×
+1×
+2×
=
.
(0.002+0.005+0.008+x+0.002)×50=1,
解得x=0.003.
(2)由(2)及题意知续驶里程在[200,300]的车辆数为:
20×(0.003×50+0.002×50)=5.
(3)由(2)及题意知,续驶里程在[200,250]的车辆数为3,
续驶里程在[250,300]的车辆数为2,
ξ的可能取值为0,1,2,
∴P(ξ=0)=
| ||
|
| 3 |
| 10 |
P(ξ=1)=
| ||||
|
| 3 |
| 5 |
P(ξ=2)=
| ||
|
| 1 |
| 10 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 3 |
| 10 |
| 3 |
| 5 |
| 1 |
| 10 |
| 4 |
| 5 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
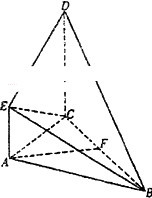 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.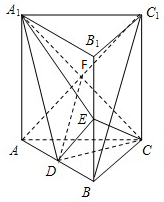 如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,
如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,