题目内容
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
(1)如果校长随机地问这个班的一名学生,下面事件发生的概率是多少?
①认为作业不多;
②喜欢玩电脑游戏并认为作业多;
(2)在认为作业多的学生中采用分层抽样的方法随机抽取5名,喜欢电脑游戏的应抽取几名?
(3)在(2)中抽取的5名中再任取2名,求恰有1名不喜欢电脑游戏的概率.
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 20 | 10 | 30 |
| 不喜欢玩电脑游戏 | 5 | 15 | 20 |
| 总数 | 25 | 25 | 50 |
①认为作业不多;
②喜欢玩电脑游戏并认为作业多;
(2)在认为作业多的学生中采用分层抽样的方法随机抽取5名,喜欢电脑游戏的应抽取几名?
(3)在(2)中抽取的5名中再任取2名,求恰有1名不喜欢电脑游戏的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(1)根据古典概率公式计算即可,
(2)根据分层抽样,计算即可,
(3)记喜欢电脑游戏的有4人分别为A,B,C,D,不喜欢电脑游戏的有1人为E,一一列举出取2名的基本事件,恰有1名不喜欢电脑游戏的基本事件,根据古典概型的概率公式计算即可.
(2)根据分层抽样,计算即可,
(3)记喜欢电脑游戏的有4人分别为A,B,C,D,不喜欢电脑游戏的有1人为E,一一列举出取2名的基本事件,恰有1名不喜欢电脑游戏的基本事件,根据古典概型的概率公式计算即可.
解答:
解:(1)①如果校长随机地问这个班的一名学生,认为作业不多的概率P=
=
,②喜欢玩电脑游戏并认为作业多的概率P=
=
;
(2)认为作业多的学生中采用分层抽样的方法随机抽取5名,喜欢电脑游戏的应抽取的人数为
×20=4名;
(3)由(2)知5名,喜欢电脑游戏的有4人,则不喜欢电脑游戏的有1人,记喜欢电脑游戏的有4人分别为A,B,C,D,不喜欢电脑游戏的有1人为E,
在这5名中再任取2名的基本事件有(AB),(AC),(AD),(AE),(BC),(BD),(BE),(CD),(CE),(DE)共10种,
恰有1名不喜欢电脑游戏有(AE),(BE),(CE),(DE)共4种,
故恰有1名不喜欢电脑游戏的概率P=
=
.
| 25 |
| 50 |
| 1 |
| 2 |
| 20 |
| 50 |
| 2 |
| 5 |
(2)认为作业多的学生中采用分层抽样的方法随机抽取5名,喜欢电脑游戏的应抽取的人数为
| 5 |
| 25 |
(3)由(2)知5名,喜欢电脑游戏的有4人,则不喜欢电脑游戏的有1人,记喜欢电脑游戏的有4人分别为A,B,C,D,不喜欢电脑游戏的有1人为E,
在这5名中再任取2名的基本事件有(AB),(AC),(AD),(AE),(BC),(BD),(BE),(CD),(CE),(DE)共10种,
恰有1名不喜欢电脑游戏有(AE),(BE),(CE),(DE)共4种,
故恰有1名不喜欢电脑游戏的概率P=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查了古典概型的概率问题,关键是一一列举出所有的基本事件,列举时不重不漏,属于基础题.

练习册系列答案
相关题目
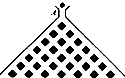 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
 如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为
如图所示,用边长为60cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个相同的小正方形,然后把四边翻折90°角,再焊接成无盖水箱,则水箱的最大容积为