题目内容
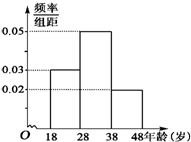 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:| 组数 | 分组 | 回答正确的人数 | 占本组的频率 |
| 第1组 | [18,28) | 240 | x |
| 第2组 | [28,38) | 300 | 0.6 |
| 第3组 | [38,48] | a | 0.4 |
(2)依据如图频率分布直方图求参与活动人群年龄的众数的估计值是多少?中位数的估计值是多少?
(3)若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48]内回答正确的得奖金200元,回答错误的得鼓励奖金20元,年龄在[18,28)内回答正确的得奖金100元,回答错误的得鼓励奖金10元,主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答问题,设该家庭获得奖金数为t元,记事件A为“数列an=-5n2+
| t-40 |
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)由频率表中第2组数据可知第2组总人数为
,再结合频率分布直方图可得a值和x值;
(2)依据上频率分布直方图可得要求的数值特征;
(3)可得父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,由题意可知该家庭获得奖金数为t元,t的值有300,210,120,30,由数列的知识可得40≤t<265,则t=120,210,可得概率.
| 300 |
| 0.6 |
(2)依据上频率分布直方图可得要求的数值特征;
(3)可得父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,由题意可知该家庭获得奖金数为t元,t的值有300,210,120,30,由数列的知识可得40≤t<265,则t=120,210,可得概率.
解答:
解:(1)由频率表中第2组数据可知第2组总人数为
=500,
再结合频率分布直方图可知n=
=1000,
∴a=1000×0.02×10×0.4=80,
∴x=
=0.8
(2)依据上频率分布直方图求参与活动人群年龄的众数的估计值在[28,38)中,
即众数的估计值为
=33,
中位数的估计值在[28,38)中,0.03×10+(t-28)×0.05=0.5,得t=32,
即中位数的估计值为32
(3)父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,
由题意可知该家庭获得奖金数为t元,t的值有300,210,120,30,
又an=-5n2+
n为递减数列,
则an+1<an对于对一切n∈N*均成立,
即-5(n+1)2+
(n+1)<-5n2+
n,
得
<10n+5对一切n∈N*均成立,
即
<15,解得40≤t<265,则t=120,210,
即父亲回答错误且孩子回答正确或父亲回答正确且孩子回答错误,
则P(A)=(1-0.4)×0.8+0.4×(1-0.8)=0.56
| 300 |
| 0.6 |
再结合频率分布直方图可知n=
| 500 |
| 0.05×10 |
∴a=1000×0.02×10×0.4=80,
∴x=
| 240 |
| 1000×0.03×10 |
(2)依据上频率分布直方图求参与活动人群年龄的众数的估计值在[28,38)中,
即众数的估计值为
| 28+38 |
| 2 |
中位数的估计值在[28,38)中,0.03×10+(t-28)×0.05=0.5,得t=32,
即中位数的估计值为32
(3)父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,
由题意可知该家庭获得奖金数为t元,t的值有300,210,120,30,
又an=-5n2+
| t-40 |
则an+1<an对于对一切n∈N*均成立,
即-5(n+1)2+
| t-40 |
| t-40 |
得
| t-40 |
即
| t-40 |
即父亲回答错误且孩子回答正确或父亲回答正确且孩子回答错误,
则P(A)=(1-0.4)×0.8+0.4×(1-0.8)=0.56
点评:本题考查古典概型及其概率公式,涉及频率分布直方图和数列,属中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
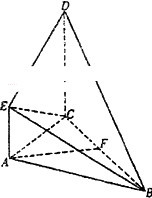 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.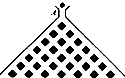 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是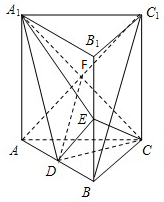 如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,
如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,