题目内容
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),若AB=2,BC=
.
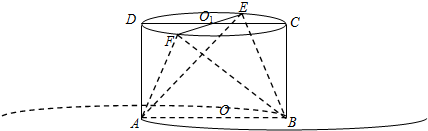
(Ⅰ)设平面BEF与⊙O所在平面的交线为l,平面ABE与⊙O1所在平面的交线为m,证明:l⊥m;
(Ⅱ)求二面角A-BE-F的平面角的余弦值.
| 2 |

(Ⅰ)设平面BEF与⊙O所在平面的交线为l,平面ABE与⊙O1所在平面的交线为m,证明:l⊥m;
(Ⅱ)求二面角A-BE-F的平面角的余弦值.
考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:空间角,空间向量及应用
分析:(Ⅰ)由已知条件推导出AB∥⊙O1所在平面,EF∥⊙O所在平面,再由EF⊥CD.能证明l⊥m.
(Ⅱ)分别以EF在⊙O所在平面内的投影、AB、OO1为坐标轴建立空间直角坐标系,利用向量法能求出二面角A-BE-F的平面角的余弦值.
(Ⅱ)分别以EF在⊙O所在平面内的投影、AB、OO1为坐标轴建立空间直角坐标系,利用向量法能求出二面角A-BE-F的平面角的余弦值.
解答:
(本小题满分12分)
解:(Ⅰ)证明:由于圆柱的两底面互相平行,
∴AB∥⊙O1所在平面,EF∥⊙O所在平面.…(2分)
∴l∥EF,m∥AB.…(4分)
而EF⊥CD.
故l⊥m.…(6分)
(Ⅱ)解:分别以EF在⊙O所在平面内的投影、AB、OO1为坐标轴建立空间直角坐标系(如图所示),
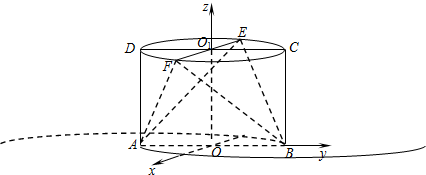
则A(0,-1,0),B(0,1,0),E(-1,0,
),F(1,0,
)…(8分)
设平面ABE的法向量分别是
=(x,y,z)
则由
•
=0及
•
=0,
得
,取z=1,得
=(
,0,1)…(10分)
设平面BEF的一个法向量为
=(0,
,1)
∵cos<
,
>=
∴所求二面角A-BE-F的平面角的余弦值为
.…(12分)
解:(Ⅰ)证明:由于圆柱的两底面互相平行,
∴AB∥⊙O1所在平面,EF∥⊙O所在平面.…(2分)
∴l∥EF,m∥AB.…(4分)
而EF⊥CD.
故l⊥m.…(6分)
(Ⅱ)解:分别以EF在⊙O所在平面内的投影、AB、OO1为坐标轴建立空间直角坐标系(如图所示),

则A(0,-1,0),B(0,1,0),E(-1,0,
| 2 |
| 2 |
设平面ABE的法向量分别是
| n1 |
则由
| n1 |
| AB |
| n1 |
| AE |
得
|
| n1 |
| 2 |
设平面BEF的一个法向量为
| n2 |
| 2 |
∵cos<
| n1 |
| n2 |
| 1 |
| 3 |
∴所求二面角A-BE-F的平面角的余弦值为
| 1 |
| 3 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f(x)(x∈R)满足f(2)=3,且f′(x)<1,则不等式f(x2)<x2+1的解集是( )
A、(-∞,-
| ||||
B、(
| ||||
C、(-
| ||||
D、(-∞,-
|
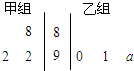 如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.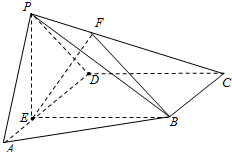 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.