题目内容
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1],a-b≠0时,有
>0成立.
(1)判断f(x)在[-1,1]上的单调性,并证明;
(2)解不等式:f(x+
)<f(
).
| f(a)-f(b) |
| a-b |
(1)判断f(x)在[-1,1]上的单调性,并证明;
(2)解不等式:f(x+
| 1 |
| 2 |
| 1 |
| x-1 |
考点:奇偶性与单调性的综合
专题:综合题,函数的性质及应用
分析:(1)根据a,b∈[-1,1],a-b≠0时,有
>0成立,利用函数单调性的定义,即可得出结论;
(2)根据f(x)在[-1,1]上单调递增,建立不等式组,即可解不等式.
| f(a)-f(b) |
| a-b |
(2)根据f(x)在[-1,1]上单调递增,建立不等式组,即可解不等式.
解答:
解:(1)f(x)在[-1,1]上单调递增.
设x1,x2∈[-1,1],x1<x2,
∵a,b∈[-1,1],a-b≠0时,有
>0成立,即对任意x1,x2∈[-1,1],有
>0,
又x1<x2,
∴f(x1)<f(x2),
∴f(x)在[-1,1]上单调递增.
(2)∵f(x)在[-1,1]上单调递增,
∴
,
∴-
≤x<-1.
设x1,x2∈[-1,1],x1<x2,
∵a,b∈[-1,1],a-b≠0时,有
| f(a)-f(b) |
| a-b |
| f(x1)-f(x2) |
| x1-x2 |
又x1<x2,
∴f(x1)<f(x2),
∴f(x)在[-1,1]上单调递增.
(2)∵f(x)在[-1,1]上单调递增,
∴
|
∴-
| 3 |
| 2 |
点评:利用函数的单调性的定义是解题的关键,借助于函数的单调性,可以转化不等式.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
tan(-
)等于( )
| 41π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
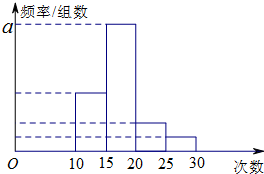 对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下:
对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下: