题目内容
已知函数f(x)=log3
(m≠1)是奇函数.
(1)求函数y=f(x)的解析式;
(2)设g(x)=
,用函数单调性的定义证明;函数y=g(x)在区间(-1,1)上单调递减;
(3)解不等式:f(t+3)<0.
| 1-x |
| 1-mx |
(1)求函数y=f(x)的解析式;
(2)设g(x)=
| 1-x |
| 1-mx |
(3)解不等式:f(t+3)<0.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,奇偶性与单调性的综合
专题:函数的性质及应用
分析:本题(1)可以由奇函数定义得到解析式满足的条件,从而求出参数m的值;
(2)利用函数单调性的定义,可以证明函数y=g(x)在区间(-1,1)上单调递减;
(3)利用(2)的结论,得到函数f(x)的单调性,再利用f(x)的单调性解不等式f(t+3)<0,得到t的取值范围,注意函数的定义域.
(2)利用函数单调性的定义,可以证明函数y=g(x)在区间(-1,1)上单调递减;
(3)利用(2)的结论,得到函数f(x)的单调性,再利用f(x)的单调性解不等式f(t+3)<0,得到t的取值范围,注意函数的定义域.
解答:
解:(1)由题意得:f(-x)+f(x)=0对于定义域中的x都成立,
∴log3
+log3
=0,
×
=1.
∴1-x2=1-mx2对于定义域中的x都成立,
∴m2=1,
∵m≠1,
∴m=-1.
∴f(x)=log3
.
(2)由(1)知:g(x)=
,
设x1,x2∈(-1,1),且x1<x2,
则x1+1>0,x2+1>0,x2-x1>0,
∵g(x1)-g(x2)=
,
∴g(x1)>g(x2),
∴函数y=g(x)在区间(-1,1)上单调递减.
(3)设函数y=f(x)的定义域为(-1,1).
设x1,x2∈(-1,1),且x1<x2,
由(2)知:g(x1)>g(x2),
∴log3g(x1)>log3g(x2),
∴f(x1)>f(x2),
∴函数y=f(x)在区间(-1,1)上单调递减.
∵f(t+3)<0=f(0),
∴
,
∴-3<t<-2.
∴不等式:f(t+3)<0的解集为:{t|-3<t<-2}.
∴log3
| 1+x |
| 1+mx |
| 1-x |
| 1-mx |
| 1+x |
| 1+mx |
| 1-x |
| 1-mx |
∴1-x2=1-mx2对于定义域中的x都成立,
∴m2=1,
∵m≠1,
∴m=-1.
∴f(x)=log3
| 1-x |
| 1+x |
(2)由(1)知:g(x)=
| 1-x |
| 1+x |
设x1,x2∈(-1,1),且x1<x2,
则x1+1>0,x2+1>0,x2-x1>0,
∵g(x1)-g(x2)=
| 2(x2-x1) |
| (1+x1)(1+x2) |
∴g(x1)>g(x2),
∴函数y=g(x)在区间(-1,1)上单调递减.
(3)设函数y=f(x)的定义域为(-1,1).
设x1,x2∈(-1,1),且x1<x2,
由(2)知:g(x1)>g(x2),
∴log3g(x1)>log3g(x2),
∴f(x1)>f(x2),
∴函数y=f(x)在区间(-1,1)上单调递减.
∵f(t+3)<0=f(0),
∴
|
∴-3<t<-2.
∴不等式:f(t+3)<0的解集为:{t|-3<t<-2}.
点评:本题考查了函数的奇偶性、单调性及其应用,本题难度不大,属于基础题.

练习册系列答案
相关题目
设曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,则a=( )
| A、0 | B、1 | C、2 | D、3 |
已知a∈R,则“a2<2a”是“a<2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
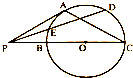 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=