题目内容
曲线y=
与直线y+2=k(x+1)有两个相异的交点,求k的范围.
| 1-(x-2)2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:将曲线方程化简,可得曲线表示以C(2,0)为圆心、半径r=1的圆的上半圆.再将直线方程化为点斜式,可得直线经过定点A(-1,-2)且斜率为k.作出示意图,设直线与半圆的切线为AD,半圆的左端点为B(1,0),当直线的斜率k小于AD的斜率且大于或等于AB的斜率时,直线与半圆有两个相异的交点.由此利用直线的斜率公式与点到直线的距离公式加以计算,可得实数k的取值范围.
解答:
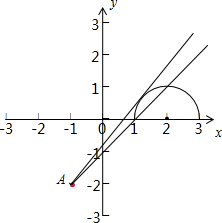 解:化简曲线y=
解:化简曲线y=
,得(x-2)2+y2=1(y≥0).
∴曲线表示以C(2,0)为圆心,半径r=1的圆的上半圆.
∵直线y+2=k(x+1)
∴直线经过定点A(-1,-2),且斜率为k.
又∵曲线y=
与直线y+2=k(x+1)有两个相异的交点,
∴设直线与半圆的切线为AD,半圆的左端点为B(1,0),
当直线的斜率k小于AD的斜率且大于或等于AB的斜率时,
直线与半圆有两个相异的交点.
由点到直线kx-y-2+k=0的距离公式,当直线与半圆相切时满足
=1,
解之得k=
,即kAD=
.
又∵直线AB的斜率kAB=
=1,
∴直线的斜率k的范围为k∈[1,
).
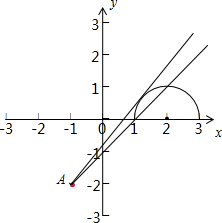 解:化简曲线y=
解:化简曲线y=| 1-(x-2)2 |
∴曲线表示以C(2,0)为圆心,半径r=1的圆的上半圆.
∵直线y+2=k(x+1)
∴直线经过定点A(-1,-2),且斜率为k.
又∵曲线y=
| 1-(x-2)2 |
∴设直线与半圆的切线为AD,半圆的左端点为B(1,0),
当直线的斜率k小于AD的斜率且大于或等于AB的斜率时,
直线与半圆有两个相异的交点.
由点到直线kx-y-2+k=0的距离公式,当直线与半圆相切时满足
| |3k-2| | ||
|
解之得k=
3+
| ||
| 4 |
3+
| ||
| 4 |
又∵直线AB的斜率kAB=
| 0+2 |
| 1+1 |
∴直线的斜率k的范围为k∈[1,
3+
| ||
| 4 |
点评:本题给出直线与半圆有两个不同的交点,求直线的斜率k的取值范围.着重考查了直线的方程、圆的方程、点到直线的距离公式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
函数f(x)=2|x|,则f(x)( )
| A、在R上是减函数 |
| B、在(-∞,0]上是减函数 |
| C、在[0,+∞)上是减函数 |
| D、在(-∞,+∞)上是增函数 |
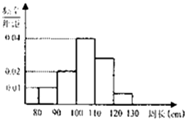 为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是
为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是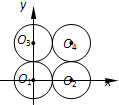 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )
如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )