题目内容
17．已知集合$A=\{y|y=\sqrt{x}\}$，B={x|y=ln（1-x）}，则A∩B=（ ）| A． | {x|0≤x＜e} | B． | {x|0≤x＜1} | C． | {x|1≤x＜e} | D． | {x|x≥0} |
分析 先分别求出集合A，B，由此利用交集定义能求出A∩B．
解答 解：∵集合$A=\{y|y=\sqrt{x}\}$={y|y≥0}，
B={x|y=ln（1-x）}={x|x＜1}，
∴A∩B={x|0≤x＜1}．
故选：B．
点评 本题考查交集合的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
特高级教师点拨系列答案
相关题目
7．函数$f（x）=\left\{\begin{array}{l}0，（x＞0）\\ π，（x=0）\\ 1，（x＜0）\end{array}\right.$，则f（f（f（π）））=（ ）
| A． | 1 | B． | 0 | C． | π | D． | π+1 |
8．已知集合P={y|y=（$\frac{1}{2}$）x，x＞0}，Q={x|y=lg（2x-x2）}，则∁RP∩Q=（ ）
| A． | [1，2） | B． | （1，+∞） | C． | [2，+∞） | D． | [1，+∞） |
2．函数$f（x）=lgx-\frac{11}{x}$的零点所在区间为（ ）
| A． | （8，9） | B． | （9，10） | C． | （10，11） | D． | （11，12） |
13．
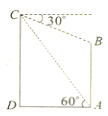如图，在热气球C正前方有一高为m的建筑物AB，在建筑物底部A测得C的仰角为60°，同时在C处测得建筑物顶部B的仰角为30°，则此时热气球的高度CD为（ ）
如图，在热气球C正前方有一高为m的建筑物AB，在建筑物底部A测得C的仰角为60°，同时在C处测得建筑物顶部B的仰角为30°，则此时热气球的高度CD为（ ）| A． | $\sqrt{2}m$ | B． | $\sqrt{3}m$ | C． | $\frac{{3\sqrt{3}}}{2}m$ | D． | $\frac{3}{2}m$ |