题目内容
17.若正数x,y满足x+2y-9=0,则$\frac{2}{y}+\frac{1}{x}$的最小值为1.分析 利用“乘1法”和基本不等式的性质即可得出.
解答 解:$\frac{2}{x}+\frac{1}{y}=\frac{1}{9}(2x+y)(\frac{2}{x}+\frac{1}{y})=\frac{1}{9}(\frac{2x}{y}+\frac{2y}{x}+5)≥1$,x=y=3时取等号.
所以$\frac{2}{x}+\frac{1}{y}$的最小值为1.
故答案为:1
点评 本题考查了“乘1法”和基本不等式的性质,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.函数$f(x)=\frac{{3{x^2}}}{{\sqrt{1-x}}}+lg(3x+1)$的定义域是( )
| A. | $\left\{x|-\frac{1}{3}<x<1\right\}$ | B. | {x|x<1} | C. | $\left\{x|x>-\frac{1}{3}\right\}$ | D. | $\left\{x|x>1或x<-\frac{1}{3}\right\}$ |
12.函数y=x-ex的增区间为( )
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
2.设全集U=R,集合$A=\{x\left|{y=\sqrt{x}}\right.\},B=\{y\left|{y={{log}_2}(x-\frac{1}{2}),x∈[1,\frac{9}{2}]}\right.\}$,则(∁UA)∩B=( )
| A. | ∅ | B. | [-1,0) | C. | $[1,\frac{9}{2}]$ | D. | [0,2] |
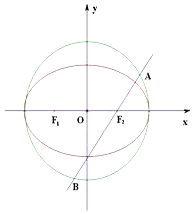 已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)
已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)