题目内容
设a,b∈R,则“
>1”是“|a|>|b|”成立的( )
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由
>1得|
|>1,所以得到|a|>|b|,而|a|>|b|时,比如a=-3,b=2,便得不出
>1,所以“
>1”是“|a|>|b|”成立的充分不必要条件.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:(1)由
>1,得|
|>1,∴|a|>|b|;
∴
>1是|a|>|b|的充分条件;
(2)若|a|>|b|,b可以取0,所以得不到
,即得不出
>1;
∴
>1不是|a|>|b|的必要条件;
所以“
>1”是“|a|>|b|”成立的充分不必要条件.
故选A.
| a |
| b |
| a |
| b |
∴
| a |
| b |
(2)若|a|>|b|,b可以取0,所以得不到
| a |
| b |
| a |
| b |
∴
| a |
| b |
所以“
| a |
| b |
故选A.
点评:考查充分条件、必要条件、充分不必要条件的概念及判断过程.

练习册系列答案
相关题目
集合{a,b,c,d}的非空真子集的个数( )
| A、16个 | B、15个 |
| C、14个 | D、13个 |
设函数f(x)=
,则f[f(4)]=( )
|
A、
| ||
| B、2 | ||
C、
| ||
| D、17 |
设f(
)=
,且f(1)=1,f(4)=7,则f(2014)=( )
| a+2b |
| 3 |
| f(a)+2f(b) |
| 3 |
| A、4026 | B、4029 |
| C、4028 | D、4027 |
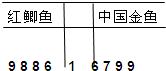 已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼.为了估计池塘中这两种鱼的数量,养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只,给每只鱼作上不影响其存活的记号,然后放回池塘,经过一定时间,再每次从池塘中随机地捕出1000只鱼,分类记录下其中有记号的鱼的数目,随即将它们放回池塘中.这样的记录作了10次.并将记录获取的数据做成以下的茎叶图,
已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼.为了估计池塘中这两种鱼的数量,养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只,给每只鱼作上不影响其存活的记号,然后放回池塘,经过一定时间,再每次从池塘中随机地捕出1000只鱼,分类记录下其中有记号的鱼的数目,随即将它们放回池塘中.这样的记录作了10次.并将记录获取的数据做成以下的茎叶图,