题目内容
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)若M(m,n)为圆C上任意一点,求
的最大值与最小值;
(3)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求当|PM|最小时的点P的坐标.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)若M(m,n)为圆C上任意一点,求
| n+2 |
| m-1 |
(3)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求当|PM|最小时的点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,直线与圆
分析:(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为-1;当切线过原点时,设切线方程为:y=kx,当切线的斜率为-1时,设切线方程为:x+y+b=0,由相切可得方程,解出即可;
(2)设k=
,则k表示直线MA的斜率,其中A(1,-2)是定点,可知直线MA与圆有公共点,从而可得
≤
,解出即可;
(3)由两点间距离公式及切线长公式,可把|PM|=|PO|化为(x+1)2+(y-2)2-2=x2+y2,化简可得x=2y-
,从而PM|=|PO|=
,可化为关于y的函数,借助二次函数的性质可求;
(2)设k=
| n+2 |
| m-1 |
| |-2k-2-2| | ||
|
| 2 |
(3)由两点间距离公式及切线长公式,可把|PM|=|PO|化为(x+1)2+(y-2)2-2=x2+y2,化简可得x=2y-
| 3 |
| 2 |
| x2+y2 |
解答:
解:圆C的方程为:(x+1)2+(y-2)2=2,
(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为-1;
当切线过原点时,设切线方程为:y=kx,相切则:
=
,得k=2±
;
当切线的斜率为-1时,设切线方程为:y+x+b=0,由相切得:
=
,得b=1或b=-3;
故所求切线方程为:y=(2+
)x或y=(2-
)x;或x+y+1=0,或x+y-3=0.
(2)设k=
,则k表示直线MA的斜率,其中A(1,-2)是定点,
∵M(m,n)在圆C,∴圆C与直线MA有公共点,
而直线MA的方程为:y+2=k(x-1),
则有:C点到直线MA的距离不大于圆C的半径即:
≤
,解得:-7≤k≤-1,
∴
的最大值为-1,最小值为-7.
(3)由圆的切线长公式可得|PM|2=|PC|2-R2=(x+1)2+(y-2)2-2,
由|PM|=|PO|得,(x+1)2+(y-2)2-2=x2+y2,即2x-4y+3=0,即x=2y-
,
此时|PM|=|PO|=
=
=
=
,
∴当y=
即P(-
,
)时,|PM|最小.
(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为-1;
当切线过原点时,设切线方程为:y=kx,相切则:
| |-k-2| | ||
|
| 2 |
| 6 |
当切线的斜率为-1时,设切线方程为:y+x+b=0,由相切得:
| |-1+2+b| | ||
|
| 2 |
故所求切线方程为:y=(2+
| 6 |
| 6 |
(2)设k=
| n+2 |
| m-1 |
∵M(m,n)在圆C,∴圆C与直线MA有公共点,
而直线MA的方程为:y+2=k(x-1),
则有:C点到直线MA的距离不大于圆C的半径即:
| |-2k-2-2| | ||
|
| 2 |
∴
| n+2 |
| m-1 |
(3)由圆的切线长公式可得|PM|2=|PC|2-R2=(x+1)2+(y-2)2-2,
由|PM|=|PO|得,(x+1)2+(y-2)2-2=x2+y2,即2x-4y+3=0,即x=2y-
| 3 |
| 2 |
此时|PM|=|PO|=
| x2+y2 |
(2y-
|
5y2-6y+
|
5(y-
|
∴当y=
| 3 |
| 5 |
| 3 |
| 10 |
| 3 |
| 5 |
点评:该题考查圆的方程、性质,考查直线与圆的位置关系,考查与圆有关的最值问题,考查转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某程序框图如图所示,该程序运行后输出S的值是( )


| A、8 | B、10 | C、31 | D、63 |
若ak=ak(k=1,2,…,2n),bk=a2k(k=1,2,…,n),且数列{ak}的所有项的和为S,则数列{bk}的所有项和S′=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
观察下面的演绎推理过程,判断正确的是( )
大前提:若直线a⊥直线 l,且直线b⊥直线 l,则a∥b.
小前提:正方体 ABCD-A1B1C1D1中,A1B1⊥AA1.且AD⊥AA1
结论:A1B1∥AD.
大前提:若直线a⊥直线 l,且直线b⊥直线 l,则a∥b.
小前提:正方体 ABCD-A1B1C1D1中,A1B1⊥AA1.且AD⊥AA1
结论:A1B1∥AD.
| A、推理正确 |
| B、大前提出错导致推理错误 |
| C、小前提出错导致推理错误 |
| D、仅结论错误 |
对实数a和b,定义运算“?”:a?b=
,设函数f(x)=x2?(x+2),x∈R,若函数y=f(x)-c的图象与x轴恰有三个公共点,则实数c的取值范围是( )
|
| A、[-1,0) |
| B、(0,1) |
| C、(-1,0) |
| D、(-1,0)∪[1,+∞) |
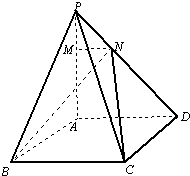 已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2
已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2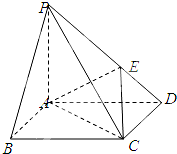 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.