题目内容
下列各组函数中,表示同一函数的是( )
A、y=1,y=
| ||||||
B、y=
| ||||||
| C、y=2x+1-2x,y=2x | ||||||
| D、y=2lgx,y=lgx2 |
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据函数的定义域相同,对应关系也相同,这样的两个函数是同一函数进行判断即可.
解答:
解:对于A,y=1(x∈R),与y=
=1(x≠0)的定义域不同,∴不是同一函数;
对于B,y=
×
=
(x≥1),
与y=
(x≥1或x≤-1)的定义域不同,∴不是同一函数;
对于C,y=2x+1-2x=2x(x∈R),与y=2x(x∈R)的定义域相同,
对应关系也相同,∴是同一函数;
对于D,y=2lgx(x>0),与y=lgx2=2lg|x|(x≠0)的定义域不同,
对应关系也不同,∴不是同一函数.
故选:C.
| x |
| x |
对于B,y=
| x-1 |
| x+1 |
| x2-1 |
与y=
| x2-1 |
对于C,y=2x+1-2x=2x(x∈R),与y=2x(x∈R)的定义域相同,
对应关系也相同,∴是同一函数;
对于D,y=2lgx(x>0),与y=lgx2=2lg|x|(x≠0)的定义域不同,
对应关系也不同,∴不是同一函数.
故选:C.
点评:本题考查了判断两个是否为同一函数的问题,解题时应判断它们的定义域是否相同,对应关系是否也相同,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,若a2=bc,则角A为( )
| A、锐角 | B、钝角 | C、直角 | D、60° |
已知函数f(x)的定义域为[1,3],则函数f(2x-1)的定义域为( )
| A、[1,2] |
| B、[1,5] |
| C、[2,4] |
| D、[1,4] |
已知a=(
)
,b=(
)
,c=
则( )
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |
 如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.
如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.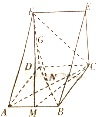 已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.
已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.