题目内容
18.若直线(a+1)x+ay=0与直线ax+2y=1垂直,则实数a=0或-3.分析 对a分类讨论,利用两条直线相互垂直的条件即可得出.
解答 解:当a=0时,两条直线方程分别化为:x=0,2y=1,此时两条直线垂直,因此a=0满足条件.
当a≠0时,两条直线的斜率分别为-$\frac{a+1}{a}$,-$\frac{a}{2}$,而-$\frac{a+1}{a}$•(-$\frac{a}{2}$)=-1,此时a=-3.
综上可得:a=0或-3.
故答案为:0或-3.
点评 本题考查了两条直线相互垂直与斜率的关系、分类讨论,属于基础题.

练习册系列答案
相关题目
13.已知圆x2+y2+2x-2y+2a=0截直线x+y+2=0所得弦长为4,则实数a的值是( )
| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
3.已知a=20.3,b=log0.23,c=log32,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | b<c<a |
8.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x3,若不等式f(-4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
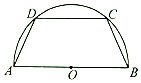 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.