题目内容
4．设集合A={x|0＜x＜1}，B={x|0＜x＜3}，那么“m∈A”是“m∈B”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 利用充要条件直接判断即可．
解答 解：集合A={x|0＜x＜1}，B={x|0＜x＜3}，那么“m∈A”⇒“m∈B”；
但是“m∈B”不能说明“m∈A”，
所以充分不必要条件．
故选：A．
点评 本题考查充要条件的判断与应用，基本知识的考查．
练习册系列答案
计算高手系列答案
相关题目
13．f（x）=$\left\{\begin{array}{l}{（3a-1）x+4a（x＜1）}\\{{a}^{x}（x≥1）}\end{array}\right.$是定义在（-∞，+∞）上是减函数，则a的取值范围是（ ）
| A． | [$\frac{1}{6}$，$\frac{1}{3}$） | B． | （0，$\frac{1}{3}$） | C． | （0，$\frac{1}{6}$] | D． | （$\frac{1}{3}$，1） |
12．在△ABC中，C＞$\frac{π}{2}$，若函数y=f（x）在[0，1]上为单调递减函数，则下列命题正确的是（ ）
| A． | f（cosA）＞f（cosB） | B． | f（sinA）＞f（sinB） | C． | f（sinA）＞f（cosB） | D． | f（sinA）＜f（cosB） |
19．已知复数z=3+$\frac{3-4i}{4+3i}$，则$\overline z$=（ ）
| A． | 3-i | B． | 2-3i | C． | 3+i | D． | 2+3i |
9．数列{an}中，${a_1}=\frac{1}{2}，{a_n}=\frac{1}{{1-{a_{n-1}}}}（n≥2，n∈N*）$，则a2015=（ ）
| A． | 2 | B． | -1 | C． | 1 | D． | $\frac{1}{2}$ |
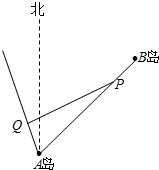已知海岛B在海岛A的北偏东45°的方向上，两岛相距10海里．小船P从海岛B以2海里/小时的速度沿直线向海岛A移动，同时小船Q从海岛A出发，沿北偏西15°方向以4海里/小时的速度移动．