题目内容

△ABC的内角A，B，C的对边分别为a，b，c．已知A，B，C成等差数列，且cosAsinC=
3
-1
4
，求内角C．
考点：两角和与差的正弦函数,等差数列的性质
专题：三角函数的求值,解三角形
分析：由已知易得A+C=120°，结合已知和三角函数公式可得A-C=30°，联立可得C值．
解答： 解：∵A，B，C成等差数列，
∴2B=A+C，又A+B+C=180°
∴B=60°，A+C=120°，①
∴sin（A-C）=sinAcosC-cosAsinC
=sinAcosC+cosAsinC-2cosAsinC
=sin（A+C）-2cosAsinC
=
3
2
-2×
3
-1
4
=
1
2

∴A-C=30°，②
由①②解得C=45°
点评：本题考查两角和与差的正弦函数，涉及等差数列和解三角形，属中档题．
练习册系列答案
相关题目
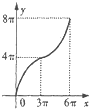
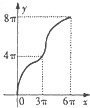
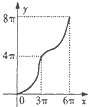
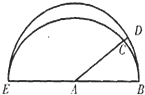如图是半径为4的半圆A与它的内切半椭圆（长半轴长为4，短半轴长为3），AD为半圆的半径，且交半椭圆于点C．现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转，设圆弧BD与AD、AB围成的面积为y，椭圆弧BC与AC、AB所围成的面积为x，则函数y=f（x）的图象大致是（　　）
A、
B、
C、
D、
已知A={（x，y）|x+y≤4，x≥0，y≥0}，B={（x，y）|0≤x≤1，0≤y≤3}，若向区域A上随机投一粒豆子，则豆子落入区域B的概率为（　　）
A、
1
4
B、
3
8
C、
1
2
D、
5
8
已知正项数列{an}的前n项和为Sn，满足Sn-an=
(an-1)2
4
．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=2nan，求数列{bn}的前n项和Tn．
若无穷数列{an}满足：①对任意n∈N*，
an+an+2
2
≤an+1；②存在常数M，对任意n∈N*，an≤M，则称数列{an}为“T数列”．
（Ⅰ）若数列{an}的通项为an=8-2n（n∈N*），证明：数列{an}为“T数列”；
（Ⅱ）若数列{an}的各项均为正整数，且数列{an}为“T数列”，证明：对任意n∈N*，an≤an+1；
（Ⅲ）若数列{an}的各项均为正整数，且数列{an}为“T数列”，证明：存在 n0∈N*，数列{an0+n}为等差数列．
对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；设函数f（x）的定义域为R+，且f（1）=3．
（Ⅰ）若（a，b）是f（x）的一个“P数对”，且f（2）=6，f（4）=9，求常数a，b的值；
（Ⅱ）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（Ⅲ）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求k的值及f（x）在区间[1，2n）（n∈N*）上的最大值与最小值．
已知正项数列{an}中，a1=t，其前n项和为Sn，满足2Sn=an•an+1．
（1）如果数列{an}为等差数列，求t的取值，并求出数列{an}的通项公式；
（2）如果数列{an}为单调递增数列，求t的取值范围．
已知函数f（x）=x|x-a|-ln（x+1）
（1）当a=0时，求函数f（x）的单调区间；
（2）当a=-1时，若?x∈[0，+∞），f（x）≤（k+1）x2恒成立，求实数k的最小值；
（3）证明：
n
i=1
2
2i-1
-ln（2n+1）＜2（n∈N*）
执行如图所示的程序框图，则输出的结果是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网