题目内容
已知A={(x,y)|x+y≤4,x≥0,y≥0},B={(x,y)|0≤x≤1,0≤y≤3},若向区域A上随机投一粒豆子,则豆子落入区域B的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:求出区域A,B的面积,利用几何概型的概率公式即可得到结论.
解答:
解:A={(x,y)|x+y≤4,x≥0,y≥0},对应三角形区域,面积为
•4•4=8;
B={(x,y)|0≤x≤1,0≤y≤3},对应矩形区域,面积为1×3=3,
∴向区域A上随机投一粒豆子,则豆子落入区域B的概率为
.
故选:B.
| 1 |
| 2 |
B={(x,y)|0≤x≤1,0≤y≤3},对应矩形区域,面积为1×3=3,
∴向区域A上随机投一粒豆子,则豆子落入区域B的概率为
| 3 |
| 8 |
故选:B.
点评:本题主要考查几何概型的概率计算,根据面积公式求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
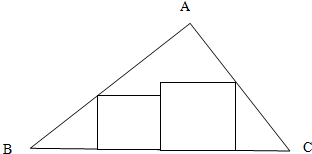
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则
如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则| BP |
| CQ |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
如图是某空间几何体的直观图,则该几何体的侧视图是( )
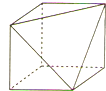

A、 |
B、 |
C、 |
D、 |
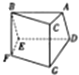 如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )
如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )