题目内容
已知函数f(x)=x|x-a|-ln(x+1)
(1)当a=0时,求函数f(x)的单调区间;
(2)当a=-1时,若?x∈[0,+∞),f(x)≤(k+1)x2恒成立,求实数k的最小值;
(3)证明:
-ln(2n+1)<2(n∈N*)
(1)当a=0时,求函数f(x)的单调区间;
(2)当a=-1时,若?x∈[0,+∞),f(x)≤(k+1)x2恒成立,求实数k的最小值;
(3)证明:
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
考点:导数在最大值、最小值问题中的应用
专题:压轴题,导数的综合应用
分析:(1)当a=0时,f(x)=x|x|-ln(x+1)(x>-1),分x∈(-1,0],x∈(0,+∞)两种情况讨论去掉绝对值符号,然后解不等式f′(x)>0,f′(x)<0可的单调区间;
(2)?x∈[0,+∞),f(x)≤(k+1)x2恒成立,可化为kx2-x+ln(x+1)≥0恒成立,令g(x)=kx2-x+ln(x+1),x≥0,则只需g(x)min≥0,当k≤0时易判断不合题意;当k>0时,利用导数可判断单调性、最值情况,进而可得结论;
(3)在(2)中取k=
,得x-ln(x+1)≤
,令h(x)=x-ln(x+1),易验证n=1时不等式成立;当n≥2时,化简可得
h(
)=
-ln(2n+1).再由h(
)≤
<
(i∈N*,i≥2),及裂项求和可得结论;
(2)?x∈[0,+∞),f(x)≤(k+1)x2恒成立,可化为kx2-x+ln(x+1)≥0恒成立,令g(x)=kx2-x+ln(x+1),x≥0,则只需g(x)min≥0,当k≤0时易判断不合题意;当k>0时,利用导数可判断单调性、最值情况,进而可得结论;
(3)在(2)中取k=
| 1 |
| 2 |
| x2 |
| 2 |
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| 2 |
| 2i-1 |
| 2 |
| (2i-1)2 |
| 2 |
| (2i-3)(2i-1) |
解答:
解:(1)当a=0时,f(x)=x|x|-ln(x+1)(x>-1),
当x∈(-1,0]时,f(x)=-x2-ln(x+1),
f′(x)=-2x-
=-
<0,
∴f(x)在x∈(-1,0]上是减函数;
当x∈(0,+∞)时,f(x)=x2-ln(x+1),
f′(x)=2x-
=
,令f'(x)>0得x>
,
∴f(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
综上得,f(x)的单调递减区间是(-1,0],(0,
),单调递增区间是(
,+∞).
(2)当a=-1时,f(x)=x|x+1|-ln(x+1)=x2+x-ln(x+1),
∴?x∈[0,+∞)时,x2+x-ln(x+1)≤(k+1)x2,即kx2-x+ln(x+1)≥0,
设g(x)=kx2-x+ln(x+1),x≥0,
当k≤0时,g(1)≤-1+ln2<0不合题意.
当k>0时,g′(x)=2kx-1+
=
,
令g'(x)=0,得x1=0,x2=
-1>-1,
①当k≥
时,x2=
-1≤0,g′(x)>0在(0,+∞)上恒成立,g(x)在[0,+∞)上单调递增,
∴g(x)≥g(0)=0,故k≥
符合题意.
②当0<k<
时,x2=
-1>0,对x∈(0,
-1),g'(x)<0,g(x)<g(0)=0,
故0<k<
不合题意,综上,k的最小值为
.
(3)在(2)中取k=
,得x-ln(x+1)≤
,令h(x)=x-ln(x+1),
证明:当n=1时,不等式左边=2-ln3<2=右边,所以不等式成立.
当n≥2时,
h(
)=
[
-ln(1+
)]
=
-
[ln(2i+1)-ln(2i-1)]
=
-ln(2n+1).
从而h(
)≤
<
(i∈N*,i≥2),
所以有
-ln(2n+1)=
h(
)=f(2)+
h(
)<2-ln3+
=2-ln3+
(
-
)=2-ln3+1-
<2.
综上,
-ln(2n+1)<2,n∈N*.
当x∈(-1,0]时,f(x)=-x2-ln(x+1),
f′(x)=-2x-
| 1 |
| x+1 |
| 2x2+2x+1 |
| x+1 |
∴f(x)在x∈(-1,0]上是减函数;
当x∈(0,+∞)时,f(x)=x2-ln(x+1),
f′(x)=2x-
| 1 |
| x+1 |
| 2x2+2x-1 |
| x+1 |
| ||
| 2 |
∴f(x)在(0,
| ||
| 2 |
| ||
| 2 |
综上得,f(x)的单调递减区间是(-1,0],(0,
| ||
| 2 |
| ||
| 2 |
(2)当a=-1时,f(x)=x|x+1|-ln(x+1)=x2+x-ln(x+1),
∴?x∈[0,+∞)时,x2+x-ln(x+1)≤(k+1)x2,即kx2-x+ln(x+1)≥0,
设g(x)=kx2-x+ln(x+1),x≥0,
当k≤0时,g(1)≤-1+ln2<0不合题意.
当k>0时,g′(x)=2kx-1+
| 1 |
| x+1 |
2kx[x+(1-
| ||
| x+1 |
令g'(x)=0,得x1=0,x2=
| 1 |
| 2k |
①当k≥
| 1 |
| 2 |
| 1 |
| 2k |
∴g(x)≥g(0)=0,故k≥
| 1 |
| 2 |
②当0<k<
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k |
故0<k<
| 1 |
| 2 |
| 1 |
| 2 |
(3)在(2)中取k=
| 1 |
| 2 |
| x2 |
| 2 |
证明:当n=1时,不等式左边=2-ln3<2=右边,所以不等式成立.
当n≥2时,
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| 2 |
| 2i-1 |
=
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| n |
 |
| i=1 |
=
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
从而h(
| 2 |
| 2i-1 |
| 2 |
| (2i-1)2 |
| 2 |
| (2i-3)(2i-1) |
所以有
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
| n |
 |
| i=2 |
| 2 |
| 2i-1 |
| n |
 |
| i=2 |
| 2 |
| (2i-3)(2i-1) |
| n |
 |
| i=2 |
| 1 |
| 2i-3 |
| 1 |
| 2i-1 |
| 1 |
| 2n-1 |
综上,
| n |
 |
| i=1 |
| 2 |
| 2i-1 |
点评:本题考查利用导数研究函数的单调性、最值,考查恒成立问题及不等式的证明,考查转化思想,考查学生综合运用知识解决复杂问题的能力,根据函数的最值、单调性构造不等式是证明不等式的关键所在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
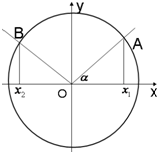 已知角α的始边与x轴的非负半轴重合,终边与单位圆O交于点A(x1,y1),将射线OA按逆时针方向旋转
已知角α的始边与x轴的非负半轴重合,终边与单位圆O交于点A(x1,y1),将射线OA按逆时针方向旋转