题目内容
若无穷数列{an}满足:①对任意n∈N*,
≤an+1;②存在常数M,对任意n∈N*,an≤M,则称数列{an}为“T数列”.
(Ⅰ)若数列{an}的通项为an=8-2n(n∈N*),证明:数列{an}为“T数列”;
(Ⅱ)若数列{an}的各项均为正整数,且数列{an}为“T数列”,证明:对任意n∈N*,an≤an+1;
(Ⅲ)若数列{an}的各项均为正整数,且数列{an}为“T数列”,证明:存在 n0∈N*,数列{an0+n}为等差数列.
| an+an+2 |
| 2 |
(Ⅰ)若数列{an}的通项为an=8-2n(n∈N*),证明:数列{an}为“T数列”;
(Ⅱ)若数列{an}的各项均为正整数,且数列{an}为“T数列”,证明:对任意n∈N*,an≤an+1;
(Ⅲ)若数列{an}的各项均为正整数,且数列{an}为“T数列”,证明:存在 n0∈N*,数列{an0+n}为等差数列.
考点:数列与不等式的综合
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)由数列{an}的通项求得an+1,an+2,作差证得对任意n∈N*,
≤an+1,结合数列{an}为递减数列得对任意n∈N*,an≤a1=6,则结论得证;
(Ⅱ)假设存在正整数k,使得ak>ak+1,由数列{an}的各项均为正整数,可得ak≥ak+1+1.然后依次推导,得到数列中有负数项,与已知矛盾;
(Ⅲ)由数列{an}为“T数列”,说明存在常数M,对任意n∈N*,an≤M.由(Ⅱ)可知,对任意n∈N*,an≤an+1,则a1≤a2≤a3≤…≤an≤an+1≤….
然后分an=an+1和若an<an+1讨论,最后说明a1,a2-a1,a3-a2,…,an-an-1,…,中最多有M个大于或等于1,否则与an≤M矛盾,则结论得到证明.
| an+an+2 |
| 2 |
(Ⅱ)假设存在正整数k,使得ak>ak+1,由数列{an}的各项均为正整数,可得ak≥ak+1+1.然后依次推导,得到数列中有负数项,与已知矛盾;
(Ⅲ)由数列{an}为“T数列”,说明存在常数M,对任意n∈N*,an≤M.由(Ⅱ)可知,对任意n∈N*,an≤an+1,则a1≤a2≤a3≤…≤an≤an+1≤….
然后分an=an+1和若an<an+1讨论,最后说明a1,a2-a1,a3-a2,…,an-an-1,…,中最多有M个大于或等于1,否则与an≤M矛盾,则结论得到证明.
解答:
(Ⅰ)证明:由an=8-2n,可得an+2=8-2n+2,an+1=8-2n+1,
∴an+an+2-2an+1=8-2n+8-2n+2-2(8-2n+1)=-2n<0,
∴对任意n∈N*,
≤an+1.
又数列{an}为递减数列,
∴对任意n∈N*,an≤a1=6.
∴数列{an}为“T数列”;
(Ⅱ)证明:假设存在正整数k,使得ak>ak+1.
由数列{an}的各项均为正整数,可得ak≥ak+1+1.
由
≤ak+1,可得ak+2≤2ak+1-ak≤2(ak-1)-ak=ak-2.
且ak+2≤2ak+1-ak<2ak+1-ak+1=ak+1.
同理ak+3<ak+1-2≤ak-3,
依此类推,可得对任意n∈N*,有ak+n≤ak-n.
因为ak为正整数,设ak=m,则m∈N*,
在ak+n≤ak-n中,设n=m,则ak+n≤0.
与数列{an}的各项均为正整数矛盾.
∴对任意n∈N*,an≤an+1;
(Ⅲ)∵数列{an}为“T数列”,
∴存在常数M,对任意n∈N*,an≤M.
设M∈N*,
由(Ⅱ)可知,对任意n∈N*,an≤an+1,
则a1≤a2≤a3≤…≤an≤an+1≤….
若an=an+1,则an+1-an=0;
若an<an+1,则an+1-an≥1.
而n≥2时,有an=a1+(a2-a1)+(a3-a2)+…+(an-an-1).
∴a1,a2-a1,a3-a2,…,an-an-1,…,中最多有M个大于或等于1,否则与an≤M矛盾.
∴存在n0∈N*,对任意的n>n0,有an-an-1=0.
∴对任意n∈N*,an0+n+1-an0+n=0.
∴存在 n0∈N*,数列{an0+n}为等差数列.
∴an+an+2-2an+1=8-2n+8-2n+2-2(8-2n+1)=-2n<0,
∴对任意n∈N*,
| an+an+2 |
| 2 |
又数列{an}为递减数列,
∴对任意n∈N*,an≤a1=6.
∴数列{an}为“T数列”;
(Ⅱ)证明:假设存在正整数k,使得ak>ak+1.
由数列{an}的各项均为正整数,可得ak≥ak+1+1.
由
| ak+ak+2 |
| 2 |
且ak+2≤2ak+1-ak<2ak+1-ak+1=ak+1.
同理ak+3<ak+1-2≤ak-3,
依此类推,可得对任意n∈N*,有ak+n≤ak-n.
因为ak为正整数,设ak=m,则m∈N*,
在ak+n≤ak-n中,设n=m,则ak+n≤0.
与数列{an}的各项均为正整数矛盾.
∴对任意n∈N*,an≤an+1;
(Ⅲ)∵数列{an}为“T数列”,
∴存在常数M,对任意n∈N*,an≤M.
设M∈N*,
由(Ⅱ)可知,对任意n∈N*,an≤an+1,
则a1≤a2≤a3≤…≤an≤an+1≤….
若an=an+1,则an+1-an=0;
若an<an+1,则an+1-an≥1.
而n≥2时,有an=a1+(a2-a1)+(a3-a2)+…+(an-an-1).
∴a1,a2-a1,a3-a2,…,an-an-1,…,中最多有M个大于或等于1,否则与an≤M矛盾.
∴存在n0∈N*,对任意的n>n0,有an-an-1=0.
∴对任意n∈N*,an0+n+1-an0+n=0.
∴存在 n0∈N*,数列{an0+n}为等差数列.
点评:本题是新定义题,考查了数列与不等式的综合,解题过程体现了反证法证题思想,关键是对“T数列”概念的理解,属有一定难度题目.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知△ABC中,角A,B,C的对边是a,b,c,且a,b,c成等比数列,则函数y=sinB+cosB的取值范围是( )
A、[-
| ||||
B、(1,
| ||||
C、[1,
| ||||
D、(0,
|
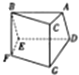 如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )
如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )