题目内容
对于函数y=f(x)与常数a,b,若f(2x)=af(x)+b恒成立,则称(a,b)为函数f(x)的一个“P数对”;设函数f(x)的定义域为R+,且f(1)=3.
(Ⅰ)若(a,b)是f(x)的一个“P数对”,且f(2)=6,f(4)=9,求常数a,b的值;
(Ⅱ)若(1,1)是f(x)的一个“P数对”,求f(2n)(n∈N*);
(Ⅲ)若(-2,0)是f(x)的一个“P数对”,且当x∈[1,2)时f(x)=k-|2x-3|,求k的值及f(x)在区间[1,2n)(n∈N*)上的最大值与最小值.
(Ⅰ)若(a,b)是f(x)的一个“P数对”,且f(2)=6,f(4)=9,求常数a,b的值;
(Ⅱ)若(1,1)是f(x)的一个“P数对”,求f(2n)(n∈N*);
(Ⅲ)若(-2,0)是f(x)的一个“P数对”,且当x∈[1,2)时f(x)=k-|2x-3|,求k的值及f(x)在区间[1,2n)(n∈N*)上的最大值与最小值.
考点:函数与方程的综合运用
专题:综合题,函数的性质及应用
分析:(Ⅰ)利用f(2)=6,f(4)=9,建立方程组,即可求常数a,b的值;
(Ⅱ)由已知,f(2x)=f(x)+1恒成立,整理f(2x)-f(x)=1,令x=2k,则f(2k+1)-f(2k)=1,{f(2k)}是等差数列,利用通项公式求解
(Ⅲ)令x=1,则f(1)=k-1=3,解得k=4,当x∈[1,2)时f(x)=4-|2x-3|,得出f(x)在[1,2)上的取值范围是[3,4].利用由已知,f(2x)=-2f(x)恒成立⊕,将[1,2n)分解成[2k-1,2k),(k∈N*)的并集,通过⊕式求出f(x)在各段[2k-1,2k)上的取值范围,各段上最大值、最小值即为所求的最大值,最小值.
(Ⅱ)由已知,f(2x)=f(x)+1恒成立,整理f(2x)-f(x)=1,令x=2k,则f(2k+1)-f(2k)=1,{f(2k)}是等差数列,利用通项公式求解
(Ⅲ)令x=1,则f(1)=k-1=3,解得k=4,当x∈[1,2)时f(x)=4-|2x-3|,得出f(x)在[1,2)上的取值范围是[3,4].利用由已知,f(2x)=-2f(x)恒成立⊕,将[1,2n)分解成[2k-1,2k),(k∈N*)的并集,通过⊕式求出f(x)在各段[2k-1,2k)上的取值范围,各段上最大值、最小值即为所求的最大值,最小值.
解答:
解:(Ⅰ)由题意知
,即
,
解得:
;…3分
(Ⅱ)由题意知f(2x)=f(x)+1恒成立,令x=2k(k∈N*),
可得f(2k+1)=f(2k)+1,∴{f(2k)}是公差为1的等差数列,
故f(2n)=f(20)+n,又f(20)=3,故f(2n)=n+3. …8分
(Ⅲ)当x∈[1,2)时,f(x)=k-|2x-3|,
令x=1,可得f(1)=k-1=3,解得k=4,…10分
所以,x∈[1,2)时,f(x)=4-|2x-3|,故f(x)在[1,2)上的取值范围是[3,4].
又(-2,0)是f(x)的一个“P数对”,故f(2x)=-2f(x)恒成立,
当x∈[2k-1,2k)(k∈N*)时,
∈[1,2),f(x)=-2f(
)=4f(
)=…=(-2)k-1f(
),…9分
故k为奇数时,f(x)在[2k-1,2k)上的取值范围是[3×2k-1,2k+1];
当k为偶数时,f(x)在[2k-1,2k)上的取值范围是[-2k+1,-3×2k-1]. …11分
所以当n=1时,f(x)在[1,2n)上的最大值为4,最小值为3;
当n为不小于3的奇数时,f(x)在[1,2n)上的最大值为2n+1,最小值为-2n;
当n为不小于2的偶数时,f(x)在[1,2n)上的最大值为2n,最小值为-2n+1.…13分.
|
|
解得:
|
(Ⅱ)由题意知f(2x)=f(x)+1恒成立,令x=2k(k∈N*),
可得f(2k+1)=f(2k)+1,∴{f(2k)}是公差为1的等差数列,
故f(2n)=f(20)+n,又f(20)=3,故f(2n)=n+3. …8分
(Ⅲ)当x∈[1,2)时,f(x)=k-|2x-3|,
令x=1,可得f(1)=k-1=3,解得k=4,…10分
所以,x∈[1,2)时,f(x)=4-|2x-3|,故f(x)在[1,2)上的取值范围是[3,4].
又(-2,0)是f(x)的一个“P数对”,故f(2x)=-2f(x)恒成立,
当x∈[2k-1,2k)(k∈N*)时,
| x |
| 2k-1 |
| x |
| 2 |
| x |
| 4 |
| x |
| 2k-1 |
故k为奇数时,f(x)在[2k-1,2k)上的取值范围是[3×2k-1,2k+1];
当k为偶数时,f(x)在[2k-1,2k)上的取值范围是[-2k+1,-3×2k-1]. …11分
所以当n=1时,f(x)在[1,2n)上的最大值为4,最小值为3;
当n为不小于3的奇数时,f(x)在[1,2n)上的最大值为2n+1,最小值为-2n;
当n为不小于2的偶数时,f(x)在[1,2n)上的最大值为2n,最小值为-2n+1.…13分.
点评:本题考查利用新定义分析问题、解决问题的能力.考查转化计算,分类讨论、构造能力及推理论证能力,思维量大,属于难题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图是某空间几何体的直观图,则该几何体的侧视图是( )
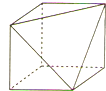

A、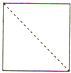 |
B、 |
C、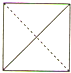 |
D、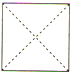 |
 近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.
近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.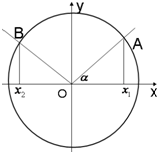 已知角α的始边与x轴的非负半轴重合,终边与单位圆O交于点A(x1,y1),将射线OA按逆时针方向旋转
已知角α的始边与x轴的非负半轴重合,终边与单位圆O交于点A(x1,y1),将射线OA按逆时针方向旋转