题目内容
已知正项数列{an}的前n项和为Sn,满足Sn-an=
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2nan,求数列{bn}的前n项和Tn.
| (an-1)2 |
| 4 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2nan,求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)利用an=sn-sn-1(n≥2),两式作差即可求得通项公式;
(Ⅱ)利用错位相减法即可求得结论.
(Ⅱ)利用错位相减法即可求得结论.
解答:
解:(Ⅰ)∵Sn-an=
.
∴4sn=
+2an+1,
4sn-1=
+2an-1+1(n≥2),
∴两式作差得an-an-1=2,又a1=1,
∴an=2n-1;
(Ⅱ)由(Ⅰ)知bn=2nan=2n(2n-1′),
∴Tn=2×1+22×3+…+2n(2n-1),①
2Tn=22×1+23×3+…+2n+1(2n-1),②
由②-①得,Tn=(2n-3)2n+1+6.
| (an-1)2 |
| 4 |
∴4sn=
| a | 2 n |
4sn-1=
| a | 2 n-1 |
∴两式作差得an-an-1=2,又a1=1,
∴an=2n-1;
(Ⅱ)由(Ⅰ)知bn=2nan=2n(2n-1′),
∴Tn=2×1+22×3+…+2n(2n-1),①
2Tn=22×1+23×3+…+2n+1(2n-1),②
由②-①得,Tn=(2n-3)2n+1+6.
点评:本题主要考查等差数列的定义及通项公式的求法、数列和的求法错位相减法等知识,考查学生的运算求解能力,属中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
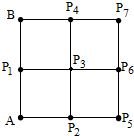 如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则
如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则| AB |
| APi |
| A、7 | B、5 | C、3 | D、1 |
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
如图是某空间几何体的直观图,则该几何体的侧视图是( )
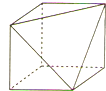

A、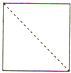 |
B、 |
C、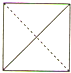 |
D、 |
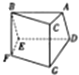 如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )
如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( ) 近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.
近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.