题目内容
设函数f(x)=sinωxcosωx-
cos2ωx(其中0<ω<3),若f(x)关于点(
,-
)对称.
(1)若f(A)=
,求锐角A;
(2)将y=f(x)的图象向左平移
ω个单位,得到y=g(x)的图象,当x∈[0,
]时,求g(x)的取值范围.
| 3 |
| π |
| 6 |
| 3 |
| 2 |
(1)若f(A)=
1-
| ||
| 2 |
(2)将y=f(x)的图象向左平移
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先通过三角函数关系式的恒等变换,变形成正弦型函数,利用函数图象的对称问题求出函数的关系式,进一步求出A的值.
(2)利用函数的平移变换求出g(x)的解析式,再利用定义域的范围求出函数的值域.
(2)利用函数的平移变换求出g(x)的解析式,再利用定义域的范围求出函数的值域.
解答:
解:(1)函数f(x)=sinωxcosωx-
cos2ωx
=
sin2ωx-
=sin(2ωx-
)-
,
由于函数f(x)关于点(
,-
)对称.
则:2ω
-
=kπ,
解得:ω=3k+1,
由于0<ω<3,
所以:k=0,
解得:ω=1.
所以:f(x)=sin(2x-
)-
,
又由于:f(A)=
,
所以:sin(2A-
)-
=
,
解得:锐角A=
.
(2)将y=f(x)的图象向左平移
个单位,得到:
g(x)=sin[2(x+
)-
]-
=sin(2x+
)-
,
由于:当x∈[0,
]时,
所以:
≤2x+
≤
,
则:
≤sin(2x+
)≤1,
≤g(x)≤1-
,
所以:g(x)的取值范围为:[
,1-
].
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2ωx-
| π |
| 3 |
| ||
| 2 |
由于函数f(x)关于点(
| π |
| 6 |
| 3 |
| 2 |
则:2ω
| π |
| 6 |
| π |
| 3 |
解得:ω=3k+1,
由于0<ω<3,
所以:k=0,
解得:ω=1.
所以:f(x)=sin(2x-
| π |
| 3 |
| ||
| 2 |
又由于:f(A)=
1-
| ||
| 2 |
所以:sin(2A-
| π |
| 3 |
| ||
| 2 |
1-
| ||
| 2 |
解得:锐角A=
| π |
| 4 |
(2)将y=f(x)的图象向左平移
| π |
| 4 |
g(x)=sin[2(x+
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
=sin(2x+
| π |
| 6 |
| ||
| 2 |
由于:当x∈[0,
| π |
| 4 |
所以:
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
则:
| 1 |
| 2 |
| π |
| 6 |
1-
| ||
| 2 |
| ||
| 2 |
所以:g(x)的取值范围为:[
1-
| ||
| 2 |
| ||
| 2 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的对称问题,三角函数的求值,函数图象的平移问题,利用三角函数的定义域求三角函数的值域.属于基础题型.

练习册系列答案
相关题目
已知x,y满足
,且z=2x+y的最大值是最小值的4倍,则a的值是( )
|
| A、4 | ||
B、
| ||
C、
| ||
D、
|
设i为虚数单位,复数
等于( )
| 2i |
| 1+i |
| A、-1+i | B、-1-i |
| C、1-i | D、1+i |
已知复数z1=3+4i,z2=t+i,且z1•z2是实数,则实数t等于( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若a>0,b>0,a+b=1,则y=
+
的最小值是( )
| 1 |
| a |
| 1 |
| b |
| A、2 | B、3 | C、4 | D、5 |
设非零向量
,
,则“
,
的夹角为锐角”是“|
+
|>|
-
|”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
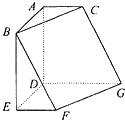 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG, 如图,已知三棱锥P-ABC中,PA⊥平面 ABC,△ABC是正三角形,AC=2 PA=2,D、E分别为棱 AC和 BC的中点.
如图,已知三棱锥P-ABC中,PA⊥平面 ABC,△ABC是正三角形,AC=2 PA=2,D、E分别为棱 AC和 BC的中点.