题目内容
函数y=log2(2x+1)的图象向右平移一个单位长度,横坐标伸长为原来的2倍,所得解析式为( )
| A、y=log2x |
| B、y=log2(2x-1) |
| C、y=log2(x+1) |
| D、y=log2(x-1) |
考点:函数解析式的求解及常用方法,函数的图象与图象变化
专题:函数的性质及应用
分析:本题可以利用函数图象平移时解析式的变化规律“左+、右-”得到相应函数的解析式,从而得到所求选项.
解答:
解:将函数y=log2(2x+1)的图象向右平移一个单位长度,
得到的图象对应的函数解析式为:y=log2[2(x-
)],
再将横坐标伸长为原来的2倍,
得到的图象对应的函数解析式为:y=
,
故选:D.
得到的图象对应的函数解析式为:y=log2[2(x-
| 1 |
| 2 |
再将横坐标伸长为原来的2倍,
得到的图象对应的函数解析式为:y=
| log | (x-1) 2 |
故选:D.
点评:本题考查的是函数图象平移与解析式的关系,要求学生能准确把握规律,细心计算.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
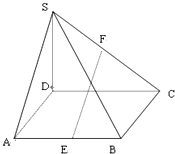 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.