题目内容
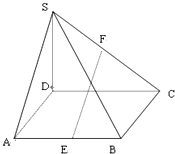 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.(1)求四棱锥S-ABCD的体积;
(2)求证:EF∥平面SAD;
(3)求异面直线AD、EF所成角的余弦值.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)根据四棱锥的体积公式即可得到结论.
(2)证明EF∥平面SAD,利用线面平行的判定,证明线线平行即可,设SD的中点为G,连接GF、AG,证明EF∥AG,即可得到结论;
(3)∠GAD(或其补角)为异面直线AD,EF所成角,在Rt△GDA中,利用余弦函数可求;
(2)证明EF∥平面SAD,利用线面平行的判定,证明线线平行即可,设SD的中点为G,连接GF、AG,证明EF∥AG,即可得到结论;
(3)∠GAD(或其补角)为异面直线AD,EF所成角,在Rt△GDA中,利用余弦函数可求;
解答:
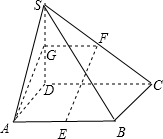 (1)解:∵SD⊥底面ABCD,四边形ABCD为矩形,且AD=SD=2,DC=3,
(1)解:∵SD⊥底面ABCD,四边形ABCD为矩形,且AD=SD=2,DC=3,
∴四棱锥S-ABCD的体积V=
×2×2×3=4.
(2)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=
CD
又E为AB的中点,故AE∥DC,AE=
CD
∴GF∥AE,且GF=AE
∴四边形AEFG为平行四边形,
∴EF∥AG.
又EF?平面SAD,AG?平面SAD
∴EF∥平面SAD
(3)解:由(2)知,EF∥AG,所以∠GAD(或其补角)为异面直线AD,EF所成角.
∵SD⊥底面ABCD,∴SD⊥DA
在Rt△GDA中,AD=2,GD=1,故GA=
,
∴cos∠GAD=
=
,
即异面直线AD,EF所成角的余弦值为
.
 (1)解:∵SD⊥底面ABCD,四边形ABCD为矩形,且AD=SD=2,DC=3,
(1)解:∵SD⊥底面ABCD,四边形ABCD为矩形,且AD=SD=2,DC=3,∴四棱锥S-ABCD的体积V=
| 1 |
| 3 |
(2)证明:设SD的中点为G,连接GF、AG,则可知GF∥DC且GF=
| 1 |
| 2 |
又E为AB的中点,故AE∥DC,AE=
| 1 |
| 2 |
∴GF∥AE,且GF=AE
∴四边形AEFG为平行四边形,
∴EF∥AG.
又EF?平面SAD,AG?平面SAD
∴EF∥平面SAD
(3)解:由(2)知,EF∥AG,所以∠GAD(或其补角)为异面直线AD,EF所成角.
∵SD⊥底面ABCD,∴SD⊥DA
在Rt△GDA中,AD=2,GD=1,故GA=
| 5 |
∴cos∠GAD=
| AD |
| AG |
2
| ||
| 5 |
即异面直线AD,EF所成角的余弦值为
2
| ||
| 5 |
点评:本题考查线面平行,考查线线角,以及棱锥的条件的计算,要求熟练掌握相应的计算公式和判定定理.

练习册系列答案
相关题目
函数y=log2(2x+1)的图象向右平移一个单位长度,横坐标伸长为原来的2倍,所得解析式为( )
| A、y=log2x |
| B、y=log2(2x-1) |
| C、y=log2(x+1) |
| D、y=log2(x-1) |
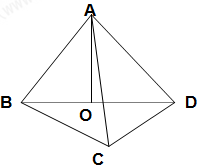 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=